1.1. Basic Elements of Dynamical Cosmology

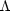Out of the many parameters which are essential for accurately determining the global dynamics and the formation history of the Universe; three clearly stand out: the Hubble constant, H₀, which tells us the expansion rate of the Universe, the matter density parameter, _m, which tells us how much matter, being baryonic or exotic, the Universe contains and the Cosmological constant, , which tells us whether the universe is filled with an extra repulsive force. The way in which these parameters affect the cosmological evolution, are determined by the gravitational field equations and the assumed equation of state. Below, I will sketch the basic framework of standard Cosmology, in order to derive the interrelations of these parameters and how they relate to the global dynamics of the Universe.

Friedmann Equations: Within the context of a homogeneous and isotropic Universe we can derive the cosmological evolution equations using either Einstein's field equations or Newtonian gravity. The latter is possible exactly because of the Cosmological Principle, ie., we can consider any volume element, as small as necessary for Newtonian gravity to apply, as being representative of the Universe as a whole. We will derive the evolution equations for the Newtonian case, using however as an active mass density:

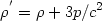
(3)

which is given within the framework of general relativity for a homogeneous and isotropic fluid with density and pressure p.

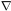
In this case we can derive the evolution equations using the mass continuity equation and Newton's equation of the motion of a small sphere. We have from the homogeneity assumption that = 0, from isotropy that 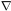^. v = 3H(t) = 3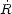 / R and then from 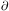/ 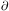t + 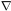^. ( v) = 0 we obtain:

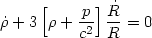
(4)

Rearranging (4) and using Newton's equation of motion, 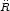= -GM / R², we have:

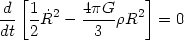
(5)

and integrating we obtain a Newtonian analogue of cosmological evolution equation:

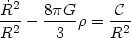
(6)

where 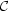is the constant of integration, which is closely related to the Newtonian energy. We can see this if we rearrange (6) as: 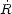² / 2 - GM/R = - 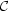/ 2. Within the relativistic formulation, the constant is in effect related to the curvature of space; 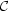= kc² and the basic equation of cosmological evolution, the Friedmann equation, is written:

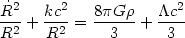
(7)

where the cosmological constant (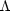) term was introduced by Einstein (rather ad hoc) in order to obtain his preferred static solution. Given an equation of state, p = p(), we can solve for and then (7) can be integrated to give R(t).

If we recall Newton's equation of motion, 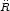= -GM / R², and we use the active density (3) and (7), we derive the second important dynamical equation of cosmological evolution. The correct relativistic form of this equation is:

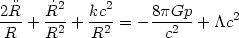
(8)

Equation of State: The question arises of which is the appropriate equation of state for the expanding Universe. The Universe expands adiabatically ⁽¹⁾, since the symmetry imposed by the Cosmological principle implies that there is no net heat flow through any surface. Therefore as it expands, it cools (11) and since it started with a very hot phase, it will be dominated, at different epochs, by different species of particles having distinct equations of state. Relativistic particles will dominate the hot phase while non-relativistic the later cooler phases.

We can specify a unique equation of state p = p() for all epochs by parameterizing it according to:

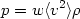
(9)

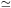where <v²> is the velocity dispersion of the fluid elements. If the dominant contribution to the density comes from relativistic particles, which have p = 1 / 3 c² (when kT >> m₀ v², with v² c²), then w = 1 / 3. If the dominant contribution comes from non-relativistic matter (when kT~ m₀v² with v² << c²) then there is negligible pressure and the dust approximation is excellent (w = 0).

Therefore inserting (9) into the mass continuity equation, (4), we obtain:

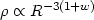
(10)

Armed with (10) one can now solve the Friedmann equation to get the time evolution of R(t), determine the age of the Universe, etc, in the different Cosmological models.

¹ An adiabatic process is defined as that in which there is no heat flow and thus the entropy is conserved (dS = 0). Back.