


2.1. Introduction
In studies of structure formation one is particularly interested in the statistical properties of the density contrast of the matter distribution,
which is defined in terms of the density field
A Fourier expansion can be made in a large enough box (of volume V) so that
where
k
We will define the power spectrum,
P(k, t), as
The dispersion of the density contrast is then simply given by
If it is assumed that for any given realization of the volume V the phases
of the Fourier coefficients
This equation implies that there is always some probability of having
After matter domination, the power spectrum of the density contrast,
where the quantities aH,
The quantity
specifies the power spectrum of density perturbations at horizon re-entry.
In the simplest inflationary models it can be well described by a single
power-law,
where n is the so-called spectral index and
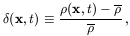
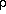 (x, t)
and the
comoving mean background density
(x, t)
and the
comoving mean background density
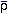 , where x
is the comoving position.
, where x
is the comoving position.
 (x, t) is
periodic within the box. We then have
(x, t) is
periodic within the box. We then have
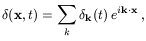
 | k | is a
comoving wavenumber, with the Fourier coefficients being given by
| k | is a
comoving wavenumber, with the Fourier coefficients being given by
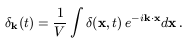
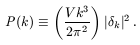
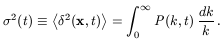
 k are uncorrelated,
the central limit theorem then guarantees that at any point the
density contrast
k are uncorrelated,
the central limit theorem then guarantees that at any point the
density contrast
 (x, t) obeys
Gaussian statistics. The
probability distribution of
(x, t) obeys
Gaussian statistics. The
probability distribution of
 (x, t) at each
point is then
(x, t) at each
point is then
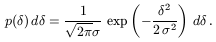
 (x, t) < - 1,
which, by definition, is not physically possible.
Therefore, as a first approximation, it is only valid to consider
(x, t) < - 1,
which, by definition, is not physically possible.
Therefore, as a first approximation, it is only valid to consider
 (x, t) as a
Gaussian random field if there is
only a very small probability of having
(x, t) as a
Gaussian random field if there is
only a very small probability of having
 (x, t) < - 1 by the
above equation, i.e. if
(x, t) < - 1 by the
above equation, i.e. if
 (t) << 1. This condition
is also
necessary if we wish to use linear perturbation theory to follow the evolution
of
(t) << 1. This condition
is also
necessary if we wish to use linear perturbation theory to follow the evolution
of
 (x, t). Gaussian
random fields are very special, since only the
power spectrum is required to specify all of the statistical properties
of the field,
whereas for non-Gaussian fields the full hierarchy of probability
distributions is needed.
(x, t). Gaussian
random fields are very special, since only the
power spectrum is required to specify all of the statistical properties
of the field,
whereas for non-Gaussian fields the full hierarchy of probability
distributions is needed.
 (x, t),
can be written as
(56,
57,
67)
(x, t),
can be written as
(56,
57,
67)
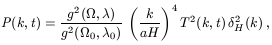
 and
and

 c2 /
3H2 are
to be calculated at t. The function
g(
c2 /
3H2 are
to be calculated at t. The function
g( ,
,
 ) accounts for the rate of
growth of density perturbations relative to the Einstein-de Sitter case,
whose growth is
given by the (aH)4 factor. The transfer function,
T(k, t), measures the change at t
in the amplitude of a perturbation with comoving wavenumber k
relative to a perturbation with infinite wavelength, thus in the limit
k -> 0 (in practice k -> khor
due to gauge ambiguities), one has T(k, t) -> 1.
The shape of the transfer function results mostly from the different
behaviour of perturbations in the radiation and matter dominated
eras, and from sub-horizon damping effects, like Silk damping,
which affects baryons, and free-streaming (Landau damping),
which acts on hot dark matter perturbations. An oscillatory pattern can also
appear in the transfer function if baryons contribute significantly to the
matter density in the Universe, due to acoustic oscillations
of the photon-baryon fluid on scales below the horizon until decoupling
occurs. The calculation of a transfer function not only depends on the
type of mechanism
responsible for the generation of the density perturbations, but also on
the assumed matter
and energy content in the Universe. It thus needs to be determined
numerically, though
nowadays there are several analytical prescriptions which approximate it
for the most popular structure formation scenarios [see e.g.
(24)].
) accounts for the rate of
growth of density perturbations relative to the Einstein-de Sitter case,
whose growth is
given by the (aH)4 factor. The transfer function,
T(k, t), measures the change at t
in the amplitude of a perturbation with comoving wavenumber k
relative to a perturbation with infinite wavelength, thus in the limit
k -> 0 (in practice k -> khor
due to gauge ambiguities), one has T(k, t) -> 1.
The shape of the transfer function results mostly from the different
behaviour of perturbations in the radiation and matter dominated
eras, and from sub-horizon damping effects, like Silk damping,
which affects baryons, and free-streaming (Landau damping),
which acts on hot dark matter perturbations. An oscillatory pattern can also
appear in the transfer function if baryons contribute significantly to the
matter density in the Universe, due to acoustic oscillations
of the photon-baryon fluid on scales below the horizon until decoupling
occurs. The calculation of a transfer function not only depends on the
type of mechanism
responsible for the generation of the density perturbations, but also on
the assumed matter
and energy content in the Universe. It thus needs to be determined
numerically, though
nowadays there are several analytical prescriptions which approximate it
for the most popular structure formation scenarios [see e.g.
(24)].
 H2(k),
defined as
H2(k),
defined as
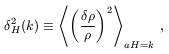
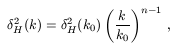
 H(k0)
is a normalisation
factor at an arbitrary comoving wavelength k0. Since
the COBE measurement of the
amplitude of the large-angle anisotropies in the temperature of the CMBR
became available, the value of
H(k0)
is a normalisation
factor at an arbitrary comoving wavelength k0. Since
the COBE measurement of the
amplitude of the large-angle anisotropies in the temperature of the CMBR
became available, the value of
 H(k0)
is usually set so as to reproduce it (though some previous
assumption has to be made regarding the contribution of
tensor perturbations, i.e. gravitational waves, to the anisotropies). When
this is done, in the simplest inflationary models the value of
H(k0)
is usually set so as to reproduce it (though some previous
assumption has to be made regarding the contribution of
tensor perturbations, i.e. gravitational waves, to the anisotropies). When
this is done, in the simplest inflationary models the value of
 H(k0)
then depends essentially only on the values of n,
H(k0)
then depends essentially only on the values of n,
 0
and
0
and 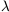 [see e.g.
(11)].
A scale-invariant, or Harrison-Zel'dovich, power spectrum corresponds to
n = 1. In general most
inflationary models give n
[see e.g.
(11)].
A scale-invariant, or Harrison-Zel'dovich, power spectrum corresponds to
n = 1. In general most
inflationary models give n
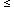 1, though in some it is possible
to have n > 1.
1, though in some it is possible
to have n > 1.