


A new kind of elementary particle has been the dominant (exclusive?) candidate for non-baryonic dark matter.
A major classification of non-baryonic dark matter is based on its temperature at the time of galaxy formation, which occurs at a photon temperature of about 1 keV. Hot dark matter was relativistic at the time of galaxy formation, and as a consequence hindered the formation of the smallest objects by streaming out of the forming structures. An example of a hot dark matter particle is a light neutrino, much lighter than ~keV. Cold dark matter was non-relativistic when galaxies formed, and thus was able to collapse effectively under the action of gravity because of its negligible pressure. Examples of cold dark matter particles are neutralinos, axions, WIMPZILLAs, solitons (B-balls and Q-balls), etc. Warm dark matter was semi-relativistic at the time of galaxy formation, and is therefore an intermediate case between hot and cold dark matter. Two examples of warm dark matter are keV-mass sterile neutrinos and gravitinos.
Another important classification of particle dark matter rests upon its production mechanism. Particles that were in thermal equilibrium in the early Universe, like neutrinos, neutralinos, and most other WIMPs (weakly interacting massive particles), are called thermal relics. Particles which were produced by a non-thermal mechanism and that never had the chance of reaching thermal equilibrium in the early Universe are called non-thermal relics. There are several examples of non-thermal relics: axions emitted by cosmic strings, solitons produced in phase transitions, WIMPZILLAs produced gravitationally at the end of inflation, etc.
For the sake of presentation, we find still another classification useful. We will divide candidates for particle dark matter into three categories: Type Ia, Type Ib, and Type II (following a common practice in superconductors and supernovas). Type Ia candidates are those known to exist, foremost among them are the neutrinos. Type Ib candidates are candidates which are still undiscovered but are `well-motivated.' By this we mean that (1) they have been proposed to solve genuine particle physics problems, a priori unrelated to dark matter, and (2) they have interactions and masses specified within a well-defined (and consistent) particle physics model. We are aware of the arbitrariness of this classification, and reserve the honor of belonging to the Type Ib category only to a sterile neutrino, the axion, and the lightest supersymmetric particle (which may be a neutralino, a gravitino, or a sneutrino) Finally, Type II candidates are all other candidates, some of which are examples of maybe fruitful ideas, such as WIMPZILLAs, solitons (B-balls, Q-balls), dark matter from extra-dimensions, self-interacting dark matter, string-inspired dark matter, string-perspired dark matter, etc. It goes without saying that a candidate may move up from Type II to Type Ib and even to Type Ia as our understanding of particle physics models progresses.
We now examine some of the current candidates.
2.1. Type Ia: candidates that exist
Dark matter candidates that are known to exist in Nature have an obvious advantage over candidates that have not been detected. The chief particles in this category are the neutrinos.
There are three known `flavors' of neutrinos: the electron neutrino
 e, the muon
neutrino
e, the muon
neutrino  µ,
and the tau neutrino
µ,
and the tau neutrino 
 . They are so
named because they are produced or destroyed in concomitance with the
electron, the muon, and the tau lepton, respectively.
. They are so
named because they are produced or destroyed in concomitance with the
electron, the muon, and the tau lepton, respectively.
"If neutrinos had a mass, they would be a good candidate for the dark matter," said Steven Hawking. We now know that neutrinos, or at least some of the neutrinos, do have a mass. This was discovered indirectly through the observation of neutrino flavor oscillations, i.e. the spontaneous conversion of one neutrino flavor into another as a neutrino propagates from point to point. The connection between flavor oscillations and neutrino masses can be seen as follows.
Consider for simplicity two flavors of neutrinos instead of three,
 e and
e and
 µ, say. Weak
interactions produce the flavor eigenstates
|
µ, say. Weak
interactions produce the flavor eigenstates
| e> and
|
e> and
| µ>, which
are associated with their respective charged leptons. However, these
flavor eigenstates are not energy eigenstates. Let
|
µ>, which
are associated with their respective charged leptons. However, these
flavor eigenstates are not energy eigenstates. Let
| 1> and
|
1> and
| 2> denote the
two energy eigenstates for the two-flavor system, with energies
E1 and E2 respectively. Then the
flavor and the energy eigenstates are connected by a unitary
transformation,
2> denote the
two energy eigenstates for the two-flavor system, with energies
E1 and E2 respectively. Then the
flavor and the energy eigenstates are connected by a unitary
transformation,
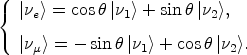 |
(5) |
Imagine that at time t = 0 we produce a
 e, so that the
initial wave function is
e, so that the
initial wave function is
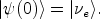 |
(6) |
After a time t, the wave function evolves according to the system
Hamiltonian 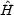 as (we
use natural units
as (we
use natural units
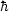 = c = 1)
= c = 1)
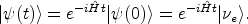 |
(7) |
To see the evolution explicitly, we expand
| e> into energy
eigenstates, and obtain
e> into energy
eigenstates, and obtain
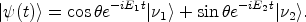 |
(8) |
We can now ask what is the probability of observing the neutrino in the
state
| µ> after a
time t, i.e. of observing a neutrino with flavor
µ> after a
time t, i.e. of observing a neutrino with flavor
 µ instead of
the initial
µ instead of
the initial  e.
According to standard rules of quantum mechanics, this probability is
e.
According to standard rules of quantum mechanics, this probability is
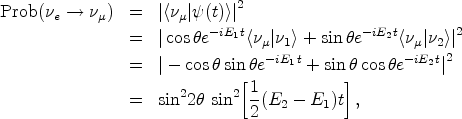 |
(9) (10) (11) (12) |
where we have used Eq. (5) and
< 1 |
1 |
 1> =
<
1> =
< 2 |
2 |
 2> = 1,
<
2> = 1,
< 1 |
1 |
 2> = 0.
For free relativistic neutrinos, with momentum p much larger than
their mass m, we have
2> = 0.
For free relativistic neutrinos, with momentum p much larger than
their mass m, we have
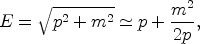 |
(13) |
and
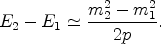 |
(14) |
Hence
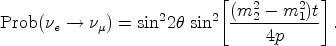 |
(15) |
This equation shows that the probability of conversion from flavor
 e to flavor
e to flavor
 µ oscillates
in time with a frequency proportional to the difference of the squares
of the neutrino masses
µ oscillates
in time with a frequency proportional to the difference of the squares
of the neutrino masses
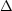 m122 = m22 -
m12. The observation of neutrino flavor
oscillations therefore implies that neutrino masses differ from each
other, and in particular that at least one of them is different from zero.
m122 = m22 -
m12. The observation of neutrino flavor
oscillations therefore implies that neutrino masses differ from each
other, and in particular that at least one of them is different from zero.
Neutrino oscillations have up to now been detected in two systems. Atmospheric muon neutrinos, which originate from the collision of cosmic rays with the Earth atmosphere, have been observed to oscillate into tau neutrinos (Fukuda et al., 1998),
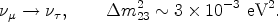 |
(16) |
Solar neutrinos, produced in the nuclear reactions that make the Sun shine, also show oscillations (Ahmad et al., 2002),
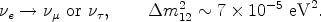 |
(17) |
These results can be used to set a lower limit on the mass of the heaviest neutrino. Indeed, the mass of the heaviest neutrino must be greater than or equal to the square root of the largest mass-squared difference (just take the mass of the other neutrino to vanish). This gives the lower limit
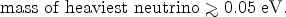 |
(18) |
Upper limits on neutrino masses come from laboratory experiments, such as tritium decay and high-energy accelerator experiments, and are (see Review of Particle Physics, Hagiwara et al., 2002)
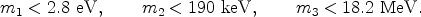 |
(19) |
However, the small mass differences implied by Eqs. (16) and (17) imply that the smallest of the three upper limits applies to all three active neutrino masses. Thus we have
 |
(20) |
It follows from this mass constraint that reactions such as
 e
e
 e
e
 e+e- in the hot early universe were
able to keep standard-model neutrinos in thermal equilibrium. The
neutrino density then follows from a computation of the neutrino number
density (see Section 2.2). The result is
e+e- in the hot early universe were
able to keep standard-model neutrinos in thermal equilibrium. The
neutrino density then follows from a computation of the neutrino number
density (see Section 2.2). The result is
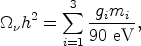 |
(21) |
where gi = 1 for a neutrino which is its own antiparticle (Majorana neutrino) and gi = 2 for a neutrino which is not its own antiparticle (Dirac neutrino).
We already mentioned in Section 1 that
cosmology provides an upper limit on the neutrino density

 h2. This translates into a cosmological upper limit on
the neutrino mass using Eq. (21). The cosmological limit is strictly
speaking on the mass density in relativistic particles at the time of
galaxy formation. An excessive amount of relativistic particles when
galaxies form, i.e. of particles with mass
m << keV, would erase too much structure at the
smallest scales. A combination of cosmic microwave background
measurements, galaxy clustering measurements, and observations of the
Lyman-
h2. This translates into a cosmological upper limit on
the neutrino mass using Eq. (21). The cosmological limit is strictly
speaking on the mass density in relativistic particles at the time of
galaxy formation. An excessive amount of relativistic particles when
galaxies form, i.e. of particles with mass
m << keV, would erase too much structure at the
smallest scales. A combination of cosmic microwave background
measurements, galaxy clustering measurements, and observations of the
Lyman- forest gives the
upper limit quoted before
(Spergel et
al., 2003)
forest gives the
upper limit quoted before
(Spergel et
al., 2003)
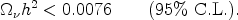 |
(22) |
Eq. (21) then gives
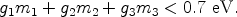 |
(23) |
On the other hand, Eq. (21) can be used in conjunction with inequality (18) to obtain a lower bound on the cosmological density in neutrinos. Taking only one massive Majorana flavor,
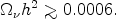 |
(24) |
Thus neutrinos are definitely a form of dark matter, although perhaps a minor component of it.
The results for the known neutrinos as dark matter can be summarized by the constraints
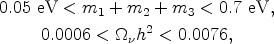 |
(25) (26) |
where the constraint in Eq. (23) has somewhat been relaxed by taking gi = 1.
The upper limit on

 h2 forbids currently known neutrinos from being the
major constituents of dark matter. Moreover, since they are light and
relativistic at the time of galaxy formation, the three neutrinos known
to exist are hot, not cold, dark matter.
h2 forbids currently known neutrinos from being the
major constituents of dark matter. Moreover, since they are light and
relativistic at the time of galaxy formation, the three neutrinos known
to exist are hot, not cold, dark matter.
The three active neutrinos are our only known particle candidates for non-baryonic dark matter. Since they fail to be cold dark matter, we are lead to consider hypothetical particles.
2.2. Type Ib: `well-motivated' candidates
We will discuss three cold dark matter candidates which are `well-motivated', i.e. that have been proposed to solve problems in principle unrelated to dark matter and whose properties can be computed within a well-defined particle physics model. The three candidates we discuss are: (1) a heavy active neutrino with standard model interactions, (2) the neutralino in the minimal supersymmetric standard model, and (3) the axion. Examples of other candidates that can be included in this category are a sterile neutrino (see, e.g., Abazajian, Fuller, & Patel, 2001) and other supersymmetric particles such as the gravitino (see, e.g., Ellis et al., 1984) and the sneutrino (see, e.g., Hall, Moroi, & Murayama, 1998).
The first two candidates we discuss belong to a general class called
weakly interacting massive particles (WIMPs).
2 WIMPs that were in
thermal equilibrium in the early universe (thermal WIMPs) are
particularly interesting. Their cosmological density is naturally of
the right order of magnitude when their interaction cross section is of
the order of a weak cross section. This also makes them detectable in
the laboratory, as we will see later. In the early Universe,
annihilation reactions that convert WIMPs into standard model particles
were initially in equilibrium with their opposite reactions. As the
universe expanded, and the temperature became smaller than the WIMP
mass, the gas of WIMPs, still in equilibrium, diluted faster than the
gas of standard model particles. This occurred because the equilibrium
number density of non-relativistic particles is suppressed by a
Boltzmann factor e-m/T with respect to the number
density of relativistic particles. After a while, WIMPs became so rare
that the WIMP annihilation reactions could no longer occur (chemical
decoupling), and from then on the number density of WIMPs decreased
inversely with volume (or in other words, the number of WIMPs per
comoving volume remained constant). Chemical decoupling occurs
approximately when the WIMP annihilation rate
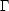 ann =
<
ann =
< ann
v>n became smaller than the universe expansion rate
H. Here
ann
v>n became smaller than the universe expansion rate
H. Here
 ann is the
WIMP annihilation cross section, v is the relative velocity of
the annihilating WIMPs, n is the WIMP number density, and the
angle brackets denote an average over the WIMP thermal
distribution. Using Friedmann's equation to find the expansion rate
H gives
ann is the
WIMP annihilation cross section, v is the relative velocity of
the annihilating WIMPs, n is the WIMP number density, and the
angle brackets denote an average over the WIMP thermal
distribution. Using Friedmann's equation to find the expansion rate
H gives
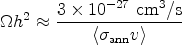 |
(27) |
for the relic density of a thermal WIMP. An important property of this equation is that smaller annihilation cross sections correspond to larger relic densities ("The weakest wins.") This can be understood from the fact that WIMPs with stronger interactions remain in chemical equilibrium for a longer time, and hence decouple when the universe is colder, wherefore their density is further suppressed by a smaller Boltzmann factor. Figure 2 illustrates this relationship.
It must be remarked here that in the non-relativistic limit v
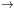 0, the product
0, the product
 ann v
tends to a constant, because the annihilation cross section
ann v
tends to a constant, because the annihilation cross section
 ann diverges
as 1/v as v
ann diverges
as 1/v as v
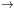 0. This is analogous
to what happens for the scattering cross section of thermal neutrons.
0. This is analogous
to what happens for the scattering cross section of thermal neutrons.
The WIMP par excellence is a heavy neutrino. The example we
consider is a thermal Dirac neutrino
 of the fourth generation with
Standard Model interactions and no lepton asymmetry.
Figure 3 summarizes its relic density as a
function of mass. Also shown in the Figure are the current constraints
from accelerator experiments and dark matter searches.
of the fourth generation with
Standard Model interactions and no lepton asymmetry.
Figure 3 summarizes its relic density as a
function of mass. Also shown in the Figure are the current constraints
from accelerator experiments and dark matter searches.
A neutrino lighter than ~ 1 MeV decouples while relativistic. If it is
so light to be still relativistic today
(m
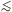 0.1 meV), its
relic density is
0.1 meV), its
relic density is
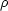
 =
7
=
7 2
T
2
T 4
/ 120. If it became non-relativistic after decoupling, its relic density
is determined by its equilibrium number density as
4
/ 120. If it became non-relativistic after decoupling, its relic density
is determined by its equilibrium number density as
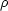
 =
m
=
m 3
3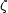 (3)
T
(3)
T 3
/ 2
3
/ 2 2. Here
T
2. Here
T =
(3/11)1/3 T
=
(3/11)1/3 T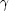 , where
T
, where
T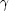 = 2.725 ± 0.002K is the cosmic microwave
background temperature. (We use natural units, c =
= 2.725 ± 0.002K is the cosmic microwave
background temperature. (We use natural units, c =
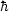 = 1.)
= 1.)
A neutrino heavier than ~ 1 MeV decouples while non-relativistic. Its
relic density is determined by its annihilation cross section, as for a
general WIMP (see Eq. (27)). The shape of the relic density curve in
Figure 3 is a reflection of the behavior of the
annihilation cross
section. The latter is dominated by the Z-boson resonance at
m
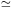 mZ /
2. This resonant annihilation gives the characteristic V shape to the
relic density curve. Above
m
mZ /
2. This resonant annihilation gives the characteristic V shape to the
relic density curve. Above
m ~ 100 GeV,
new annihilation channels open up, namely the annihilation of two
neutrinos into two Z- or W-bosons. The new channels increase the
annihilation cross section and thus lower the neutrino relic
density. Soon, however, the perturbative expansion of the cross section
in powers of the (Yukawa) coupling constant becomes untrustworthy (the
question mark in Figure 3). An alternative
unitarity argument limits the Dirac neutrino relic density to the dashed
curve on the right in the Figure. Neutrinos heavier than 10 TeV
`overclose' the universe, i.e. have a relic density that corresponds to
a universe which is too young.
~ 100 GeV,
new annihilation channels open up, namely the annihilation of two
neutrinos into two Z- or W-bosons. The new channels increase the
annihilation cross section and thus lower the neutrino relic
density. Soon, however, the perturbative expansion of the cross section
in powers of the (Yukawa) coupling constant becomes untrustworthy (the
question mark in Figure 3). An alternative
unitarity argument limits the Dirac neutrino relic density to the dashed
curve on the right in the Figure. Neutrinos heavier than 10 TeV
`overclose' the universe, i.e. have a relic density that corresponds to
a universe which is too young.
The `dark matter' band in Figure 3 indicates
where the neutrino is a good dark matter candidate (the band is actually
quite generous in light of the most recent measurements of
 h2). A thermal Dirac neutrino is a good dark matter
candidate when its mass is around few eV, a few GeV or possibly a
TeV. For masses smaller than about an eV and between ~ 10 GeV and ~ 100
GeV, it is an underabundant relic from the Big Bang, too dilute to be a
major component of the dark matter but nevertheless a cosmological
relic. For other masses, it is cosmologically excluded.
h2). A thermal Dirac neutrino is a good dark matter
candidate when its mass is around few eV, a few GeV or possibly a
TeV. For masses smaller than about an eV and between ~ 10 GeV and ~ 100
GeV, it is an underabundant relic from the Big Bang, too dilute to be a
major component of the dark matter but nevertheless a cosmological
relic. For other masses, it is cosmologically excluded.
Dark matter neutrinos with a mass around 1 eV would be relativistic at the time of galaxy formation (~ keV), and would thus be part of hot dark matter. From the bounds on hot dark matter in the preceding Section, however, they cannot be a major component of the dark matter in the Universe.
Neutrinos can be cold dark matter if their masses are around few GeV or a TeV. However, fourth-generation heavy neutrinos lighter than 45 GeV are excluded by the measurement of the Z-boson decay width at the Large Electron-Positron collider at CERN. Moreover, direct searches for WIMP dark matter in our galaxy exclude Dirac neutrinos heavier than ~ 0.5 GeV as the dominant component of the galactic dark halo (see Figure 3). Thus although heavy Dirac neutrinos could still be a tiny part of the halo dark matter, they cannot solve the cold dark matter problem.
We need another non-baryonic candidate for cold dark matter.
The WIMP par default is the lightest neutralino
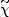 10, or sometimes simply
10, or sometimes simply
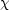 , which is often the
lightest supersymmetric particle in supersymmetric extensions of the
Standard Model of particle physics. Supersymmetry is a new symmetry of
space-time that has been discovered in the process of unifying the
fundamental forces of nature (electroweak, strong, and
gravitational). Supersymmetry also helps in stabilizing the masses of
fundamental scalar particles in the theory, such as the Higgs boson, a
problem, called the hierarchy problem, which basically consists in
explaining why gravity is so much weaker than the other forces.
, which is often the
lightest supersymmetric particle in supersymmetric extensions of the
Standard Model of particle physics. Supersymmetry is a new symmetry of
space-time that has been discovered in the process of unifying the
fundamental forces of nature (electroweak, strong, and
gravitational). Supersymmetry also helps in stabilizing the masses of
fundamental scalar particles in the theory, such as the Higgs boson, a
problem, called the hierarchy problem, which basically consists in
explaining why gravity is so much weaker than the other forces.
Of importance for cosmology is the fact that supersymmetry requires the existence of a new particle for each particle in the Standard Model. These supersymmetric partners differ by half a unit of spin, and come under the names of sleptons (partners of the leptons), squarks (partners of the quarks), gauginos (partners of the gauge bosons) and higgsinos (partners of the Higgs bosons). Sleptons and squarks have spin 0, and gauginos and higgsinos have spin 1/2.
If supersymmetry would be an explicit symmetry of nature, superpartners would have the same mass as their corresponding Standard Model particle. However, no Standard Model particle has a superpartner of the same mass. It is therefore assumed that supersymmetry, much as the weak symmetry, is broken. Superpartners can then be much heavier than their normal counterparts, explaining why they have not been detected so far. However, the mechanism of supersymmetry breaking is not completely understood, and in practice it is implemented in the model by a set of supersymmetry-breaking parameters that govern the values of the superpartners masses (the superpartners couplings are fixed by supersymmetry).
The scenario with the minimum number of particles is called the minimal
supersymmetric standard model or MSSM. The MSSM has 106 parameters
beyond those in the Standard Model: 102 supersymmetry-breaking
parameters, 1 complex supersymmetric parameter µ, and 1
complex electroweak symmetry-breaking parameter
tan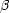 (see,
e.g., the article by Haber in Review of Particle Physics,
Hagiwara et al., 2002).
Since it is cumbersome to work with so many parameters, in practice
phenomenological studies consider simplified scenarios with a
drastically reduced number of parameters. The most studied case (not
necessarily the one Nature has chosen) is minimal supergravity, which
reduces the number of parameters to five: three real mass parameters at
the Grand Unification scale (the scalar mass m0, the
scalar trilinear coupling A0, and the gaugino mass
m1/2) and two real parameters at the weak scale (the
ratio of Higgs expectation values
tan
(see,
e.g., the article by Haber in Review of Particle Physics,
Hagiwara et al., 2002).
Since it is cumbersome to work with so many parameters, in practice
phenomenological studies consider simplified scenarios with a
drastically reduced number of parameters. The most studied case (not
necessarily the one Nature has chosen) is minimal supergravity, which
reduces the number of parameters to five: three real mass parameters at
the Grand Unification scale (the scalar mass m0, the
scalar trilinear coupling A0, and the gaugino mass
m1/2) and two real parameters at the weak scale (the
ratio of Higgs expectation values
tan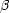 and the
sign of the µ parameter). Other scenarios are possible and
are considered in the literature. Of relevance to dark matter studies
is, for example, a class of models with seven parameters specified at
the weak scale: µ,
tan
and the
sign of the µ parameter). Other scenarios are possible and
are considered in the literature. Of relevance to dark matter studies
is, for example, a class of models with seven parameters specified at
the weak scale: µ,
tan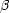 , the
gaugino mass parameter
M2, the mass mA of the CP-odd Higgs
boson, the sfermion mass parameter
, the
gaugino mass parameter
M2, the mass mA of the CP-odd Higgs
boson, the sfermion mass parameter
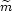 , the bottom and top
quark trilinear couplings Ab and
At. See the reviews by
Jungman,
Kamionkowski & Griest (1996) and
Bergström (2000)
for more details.
, the bottom and top
quark trilinear couplings Ab and
At. See the reviews by
Jungman,
Kamionkowski & Griest (1996) and
Bergström (2000)
for more details.
It was realized long ago by Goldberg (1983) and Ellis et al. (1984) that the lightest superposition of the neutral gauginos and the neutral higgsinos (which having the same quantum numbers mix together) is an excellent dark matter candidate. It is often the lightest supersymmetric particle, it is stable under the requirement that superpartners are only produced or destroyed in pairs (called R-parity conservation), it is weakly interacting, as dictated by supersymmetry, and it is massive. It is therefore a genuine WIMP, and it is among the most studied of the dark matter candidates. Its name is the lightest neutralino.
Several calculations exist of the density of the lightest neutralino. An
example is given in Figure 4, which reproduces a
figure from
Edsjö &
Gondolo (1997),
updated with the WMAP value of the cold dark matter density. This figure
was obtained in a scenario with seven supersymmetric parameters at the
weak scale. The relic density is not fixed once the neutralino mass is
given, as was the case for a Dirac neutrino, because the neutralino
annihilation cross section depends on the masses and composition of many
other supersymmetric particles, thus ultimately on all supersymmetric
parameters. Therefore the density in Figure 4 is
not a single-valued
function of the neutralino mass, and the plot must be obtained through
an extended computer scan in the seven-dimensional parameter space.
3 It is clear from
Figure 4 that it is possible to choose the
values of the supersymmetric parameters in a way that the neutralino
relic density satisfies the current determination of
 h2. Although it may seem ridiculous to claim that the
neutralino is naturally a good dark matter candidate, let us
notice that the neutralino relic density in Figure
4 and the neutrino relic density in Figure 3
have a similar range of variation. It is the precision of the
cosmological measurements that make us think otherwise.
h2. Although it may seem ridiculous to claim that the
neutralino is naturally a good dark matter candidate, let us
notice that the neutralino relic density in Figure
4 and the neutrino relic density in Figure 3
have a similar range of variation. It is the precision of the
cosmological measurements that make us think otherwise.
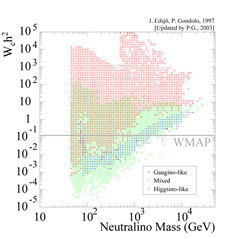 |
Figure 4. Relic density of the lightest neutralino as a function of its mass. For each mass, several density values are possible depending on the other supersymmetric parameters (seven in total in the scenario plotted). The color code shows the neutralino composition (gaugino, higgsino or mixed). The gray horizontal line is the current error band in the WMAP measurement of the cosmological cold dark matter density. (Figure adapted from Edsjö & Gondolo, 1997.) |
Reversing the argument, the precision of the cosmological measurements can be used to select the regions of supersymmetric parameter space where the lightest neutralino is cold dark matter. With the current precision of cosmological measurements, these are very thin regions in supersymmetric parameter space. For this approach to be carried out properly, the theoretical calculation of the neutralino relic density should match the precision of the cosmological data. The latter is currently 7%, as can be gathered from Eq. (4), and is expected to improve to about 1% before the end of the decade with the launch of the Planck mission. A calculation of the neutralino relic density good to 1% now exists, and is available in a computer package called DarkSUSY (Gondolo et al., 2002, 2000). The 1% precision refers to the calculation of the relic density starting from the supersymmetric parameters at the weak scale. The connection with the parameters at the Grand Unification scale, which is vital for minimal supergravity, introduces instead large errors in important regions of parameter space, errors that some authors estimate to be as big as 50% (Allanach, Kraml, & Porod, 2003).
Given the importance of this calculation, we give now a rapid survey of the ingredients needed to achieve a precision of 1%. Firstly, the equation governing the evolution of the neutralino number density n,
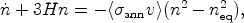 |
(28) |
has to be solved numerically. The equation being `stiff' (i.e. its
difference equation being stable only for unreasonably small
stepsizes), a special numerical method should be used. The thermal
average of the annihilation cross section
< ann
v> at temperature T should be computed
relativistically, since the typical speed of neutralinos at decoupling
is of the order of the speed of light,
v ~ c / 3. For this purpose, we can use the expression in
Gondolo &
Gelmini (1991):
ann
v> at temperature T should be computed
relativistically, since the typical speed of neutralinos at decoupling
is of the order of the speed of light,
v ~ c / 3. For this purpose, we can use the expression in
Gondolo &
Gelmini (1991):
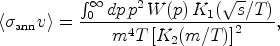 |
(29) |
where W(p) is the annihilation rate per unit volume and
unit time (a relativistic invariant),
s = 4(m2 + p2) is the
center-of-mass energy squared, and K1,
K2 are modified Bessel functions. In passing, let us
remark that the common method of expanding in powers of
v2,
 ann v
= a + bv2 + ... , and then taking
the thermal average to give
<
ann v
= a + bv2 + ... , and then taking
the thermal average to give
< ann
v> = a + b(3T / 2m) +
... is unreliable, since it gives rise to negative
<
ann
v> = a + b(3T / 2m) +
... is unreliable, since it gives rise to negative
< ann
v>, and thus negative
ann
v>, and thus negative
 h2, near resonances and thresholds. These are nowadays
the most important regions of parameter space. Finally, an essential
ingredient in the calculation of the neutralino relic density is the
inclusion of coannihilation processes. These are processes that deplete
the number of neutralinos through a chain of reactions, and occur when
another supersymmetric particle is close in mass to the lightest
neutralino (
h2, near resonances and thresholds. These are nowadays
the most important regions of parameter space. Finally, an essential
ingredient in the calculation of the neutralino relic density is the
inclusion of coannihilation processes. These are processes that deplete
the number of neutralinos through a chain of reactions, and occur when
another supersymmetric particle is close in mass to the lightest
neutralino (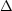 m
~ T). In this case, scattering of the neutralino off a particle
in the thermal `soup' can convert the neutralino into the other
supersymmetric particle close in mass, given that the energy barrier
that would otherwise have prevented it (i.e. the mass difference) is
easily overcome. The supersymmetric particle participating in the
coannihilation may then decay and/or react with other particles and
eventually effect the disappearance of neutralinos. We give two
examples. Coannihilation with charginos
m
~ T). In this case, scattering of the neutralino off a particle
in the thermal `soup' can convert the neutralino into the other
supersymmetric particle close in mass, given that the energy barrier
that would otherwise have prevented it (i.e. the mass difference) is
easily overcome. The supersymmetric particle participating in the
coannihilation may then decay and/or react with other particles and
eventually effect the disappearance of neutralinos. We give two
examples. Coannihilation with charginos
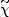 ±
(partners of the charged gauge and Higgs bosons) may proceed via, for
instance,
±
(partners of the charged gauge and Higgs bosons) may proceed via, for
instance,
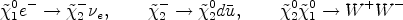 |
(30) |
(subscripts on superpartner names indicate particles with different
masses). Coannihilation with tau sleptons
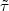 may instead
involve the processes
may instead
involve the processes
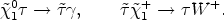 |
(31) |
Coannihilations were first included in the study of near-degenerate heavy neutrinos by Binetruy, Girardi, & Salati (1984) and were brought to general attention by Griest & Seckel (1991). The current state-of-the-art treatment of neutralino coannihilations, which involves several thousands of processes, is contained in the work by Edsjö & Gondolo (1997) and Edsjö, Schelke, Ullio, & Gondolo (2003).
To illustrate the power of the cosmological precision measurements in
selecting regions of supersymmetric parameter space,
Figure 5 shows the WMAP constraint in one of the
figures in
Edsjö, Schelke, Ullio, &
Gondolo (2003).
The constraint is as a very thin line that approximately follows the
edges of the allowed region in this slice of parameter space (the
m0-m1/2 plane with µ
< 0, tan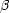 =
30 and A0 = 0).
=
30 and A0 = 0).
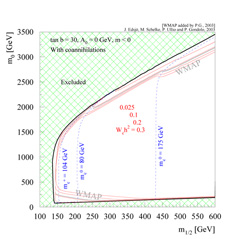 |
Figure 5. Illustration of the power of WMAP
constraints on the minimal supergravity parameter space. The figure
shows a slice in m0 and m1/2 with
µ < 0 at
tan |
Cosmological constraints on supersymmetric models are very powerful, and may even serve as a guidance in searching for supersymmetry. This partially justifies the extensive literature on the subject. The neutralino as dark matter is certainly `fashionable.'
Our third and last example of a `well-motivated' cold dark matter candidate is the axion.
Axions were suggested by Peccei & Quinn (1977) to solve the so-called "strong CP problem". Out of the vacuum structure of Quantum Chromodynamics there arises a large CP-violating phase, which is at variance with stringent measurements of the electric dipole moment of the neutron, for example. A possible solution to this problem is that the CP-violating phase is the vacuum expectation value of a new field, the axion, which relaxes dynamically to a very small value. The original axion model of Peccei and Quinn is today experimentally ruled out, but other axion models based on the same idea have been proposed. Among them are the invisible axions of Kim (1979) and Shifman, Vainshtein, & Zakharov (1980) (KSVZ axion) and of Dine, Fischler, & Srednicki (1981) and Zhitnitsky (1980) (DFSZ). They differ in the strength of the axion couplings to matter and radiation.
In a cosmological context, axions, contrary to neutrinos and neutralinos, are generally produced non-thermally (although thermal axion production is sometimes considered, as are non-thermal neutrino and neutralino productions). The two main mechanisms for non-thermal axion production are vacuum alignment and emission from cosmic strings. In the vacuum alignment mechanism, a potential is generated for the axion field at the chiral symmetry breaking, and the axion field, which can in principle be at any point in this potential, starts moving toward the minimum of the potential and then oscillates around it. Quantum-mechanically, the field oscillations correspond to the generation of axion particles. In the other main non-thermal mechanism for axion production, axions are emitted in the wiggling or decay of cosmic strings. In both cases, axions are produced with small momentum, << keV, and thus they are cold dark matter despite having tiny masses, between 1 µeV and 1 meV. This is in fact the range of masses in which axions are good dark matter candidates. Figure 6 shows the current constraints on the axion mass from laboratory, astrophysical, and cosmological data.
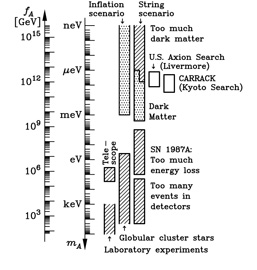 |
Figure 6. Laboratory, astrophysical, and
cosmological constraints on the axion mass mA. The
inflation scenario and the string scenario are referred in the text as
the vacuum alignment scenario and the string emission scenario,
respectively. fA is the axion decay constant, which
is inversely related to mA. The axion is a good dark
matter candidate for 1 µeV
|
Searches for axions as galactic dark matter rely on the coupling of axions to two photons. An incoming galactic axion can become a photon in the magnetic field in a resonant cavity. For this to happen, the characteristic frequency of the cavity has to match the axion mass. Since the latter is unknown, searches for galactic axions use tunable cavities, and scan over the cavity frequency, a time-consuming process. The U.S. axion search at Livermore is currently exploring a wide range of interesting axion masses, and has put some constraint on the KSVZ axion as a dominant component of the galactic halo (Asztalos et al., 2004). Figure 7 shows the constraints on the local galactic density in axions as a function of the axion mass. KSVZ axions with mass in the range 1.91-3.34 µeV cannot be the main component of galactic dark matter. The Livermore search is still continuing to a larger range of axion masses. It is fair to say that axion dark matter is either about to be detected or about to be ruled out.
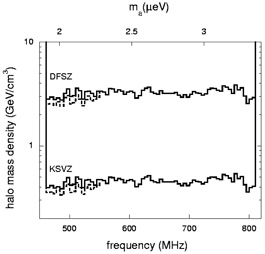 |
Figure 7. Experimental constraints on the density of axions in the galactic halo near the Sun as a function of the axion mass (upper scale) and cavity frequency (lower scale). The regions above the curves marked `DFSZ' and `KSVZ' are excluded fro the respective axion models. The currently accepted value for the local dark halo density is 0.45 GeV/cm3, which is approximately the extension of the excluded region for the KSVZ axion. (Figure from Asztalos et al., 2004.) |
2.3. Type II: other candidates
In the Type II category we put all hypothetical cold dark matter candidates that are neither Type Ia nor Type Ib. Some of these candidates have been proposed for no other reason than to solve the dark matter problem. Others are examples of beautiful ideas and clever mechanisms that can provide good possibilities for non-baryonic dark matter, but in some way or another lack the completeness of the theoretical particle physics models of Types Ia and Ib. Although Type II candidates are not studied as deeply as others, it may well be that eventually the question of the nature of cold dark matter might find its answer among them.
Below we present the idea of self-interacting dark matter and gravitationally-produced WIMPZILLAs. Other interesting candidates have been proposed recently in models with extra dimensions, such as Kaluza-Klein dark matter (Cheng, Feng, & Matchev, 2002) and branons (Cembranos, Dobado, & Maroto, 2003).
There are several ways in which one may be able to come up with an ad hoc candidate for non-baryonic cold dark matter. A humorous flowchart on how to do this was put together around 1986 by a group of graduate students at Princeton (Lauer, Statler, Ryden, & Weinberg, 1986). The flowchart involves multiple options, and one possibility runs as follows. "A new particle is envisioned which is cooked up just to make everything OK but violates federal law ...still, it doesn't prevent a paper being written by Spergel ..." We have now the proper setting to introduce a candidate suggested by Spergel & Steinhardt (2000), self-interacting dark matter.
The idea behind the introduction of self-interacting dark matter is to
find a solution to the cusp and satellite problems of standard cold dark
matter scenarios. These two problems are in effect discrepancies between
observations and results of simulations of structure formation on the
galactic scale. Namely, in the cusp problem, numerical simulations
predict a dark matter density profile which increases toward the center
of a galaxy like a power law
r- with
with
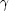 ~ 1 or
higher. This sharp density increase is called a cusp. On the other hand,
kinematical and dynamical determinations of the dark matter profile in
the central regions of galaxies, especially of low surface brightness
galaxies, tend not to show such a sharp increase but rather a constant
density core. The observational situation is still rather confused, with
some galaxies profiles being compatible with a cusp and others with a
core. The theoretical situation is also not fully delineated, with
higher resolution simulations showing a dependence of the slope
~ 1 or
higher. This sharp density increase is called a cusp. On the other hand,
kinematical and dynamical determinations of the dark matter profile in
the central regions of galaxies, especially of low surface brightness
galaxies, tend not to show such a sharp increase but rather a constant
density core. The observational situation is still rather confused, with
some galaxies profiles being compatible with a cusp and others with a
core. The theoretical situation is also not fully delineated, with
higher resolution simulations showing a dependence of the slope
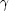 on the
mass of the galaxy. Although many ideas have been proposed for the
resolution of the cusp problem, it is still not completely resolved.
on the
mass of the galaxy. Although many ideas have been proposed for the
resolution of the cusp problem, it is still not completely resolved.
Perhaps connected with the cusp problem is the satellite problem, which is a mismatch between the observed and the simulated numbers of satellites in a galaxy halo. Too many satellites are predicted by the simulations. In reality, observations can detect only the luminous satellites while simulations contain all satellites, including the dark ones. It may be that many dark satellites do not shine, thus solving the satellite problem, but how and which satellites become luminous is not understood yet.
Spergel &
Steinhardt (2000)
suggested another way to solve both problems. They realized that if dark
matter particles would interact with each other with a mean free path of
the order of the size of galactic cores, the dark matter interactions
would efficiently thermalize the system and avoid the formation of both
a central cusp and too many satellites. The requirement on the mean free
path
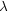 is roughly
is roughly
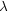 ~ 10 kpc. We can
figure out the necessary cross section
~ 10 kpc. We can
figure out the necessary cross section
 for dark matter
self-interactions by recalling that the mean free path is related to the
cross section and the number density n, or matter density
for dark matter
self-interactions by recalling that the mean free path is related to the
cross section and the number density n, or matter density
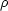 = mn,
through the relationship
= mn,
through the relationship
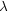 = 1 /
(n
= 1 /
(n ) = m /
(
) = m /
(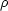
 ). Taking a typical
). Taking a typical
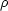 ~ 0.3
GeV/cm3 gives
~ 0.3
GeV/cm3 gives
 / m ~ 60
cm2/g. So
Spergel &
Steinhardt (2000)
suggested a new self-interacting dark matter particle with
/ m ~ 60
cm2/g. So
Spergel &
Steinhardt (2000)
suggested a new self-interacting dark matter particle with
 / m in the range
/ m in the range
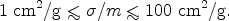 |
(32) |
To understand the magnitude of this number, it is useful to compare it with the geometric cross section of a proton, which is one of the largest known cross sections for elementary particles. We have
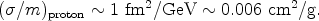 |
(33) |
Thus the desired  /
m seems rather big. It is therefore not surprising that
astrophysical constraints on self-interacting dark matter are rather
stringent.
Gnedin &
Ostriker (2001)
considered the evaporation of halos inside clusters and set the
constraint
/
m seems rather big. It is therefore not surprising that
astrophysical constraints on self-interacting dark matter are rather
stringent.
Gnedin &
Ostriker (2001)
considered the evaporation of halos inside clusters and set the
constraint
 / m < 0.3-1
cm2/g.
Yoshida,
Springel, White, & Tormen (2000)
considered the shape of cluster cores, which is rounder for
self-interacting dark matter than for standard cold dark matter, and
concluded that
/ m < 0.3-1
cm2/g.
Yoshida,
Springel, White, & Tormen (2000)
considered the shape of cluster cores, which is rounder for
self-interacting dark matter than for standard cold dark matter, and
concluded that  /
m must be < 10 cm2/g. This bound was later
strengthened by
Miralda-Escudé (2002) to
/
m must be < 10 cm2/g. This bound was later
strengthened by
Miralda-Escudé (2002) to
 / m < 0.02
cm2/g.
Markevitch
et al. (2003)
discovered a gas bullet lagging behind dark matter in the merging galaxy
cluster 1E0657-56. They combined Chandra X-ray maps of the hot gas in
the cluster with weak lensing maps of its mass distribution. From
estimates of the column mass densities and of the distance between the
gas and the dark matter, Markevitch et al. were able to set the upper
limit
/ m < 0.02
cm2/g.
Markevitch
et al. (2003)
discovered a gas bullet lagging behind dark matter in the merging galaxy
cluster 1E0657-56. They combined Chandra X-ray maps of the hot gas in
the cluster with weak lensing maps of its mass distribution. From
estimates of the column mass densities and of the distance between the
gas and the dark matter, Markevitch et al. were able to set the upper
limit
 / m < 10
cm2/g with direct observations of the dark matter
distribution. All these bounds leave little room, if any, to
self-interacting dark matter a la Spergel & Steinhardt.
/ m < 10
cm2/g with direct observations of the dark matter
distribution. All these bounds leave little room, if any, to
self-interacting dark matter a la Spergel & Steinhardt.
Our last example of cold dark matter candidates illustrates a fascinating idea for generating matter in the expanding universe: the gravitational creation of matter in an accelerated expansion. This mechanism is analogous to the production of Hawking radiation around a black hole, and of Unruh radiation in an accelerated reference frame.
WIMPZILLAs
(Chung, Kolb,
& Riotto, 1998,
1999;
Kuzmin &
Tkachev, 1998)
are very massive relics from the Big Bang, which can be the dark matter
in the universe if their mass is
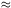 1013
GeV. They were produced at the end of inflation through a variety of
possible mechanisms: gravitationally, during preheating, during
reheating, in bubble collisions. It is possible that their relic
abundance does not depend on their interaction strength but only on
their mass, giving great freedom in their phenomenology. To be the dark
matter today, they are assumed to be stable or to have a lifetime of the
order of the age of the universe. In the latter case, their decay
products may give rise to the highest energy cosmic rays, and solve the
problem of cosmic rays beyond the GZK cutoff.
1013
GeV. They were produced at the end of inflation through a variety of
possible mechanisms: gravitationally, during preheating, during
reheating, in bubble collisions. It is possible that their relic
abundance does not depend on their interaction strength but only on
their mass, giving great freedom in their phenomenology. To be the dark
matter today, they are assumed to be stable or to have a lifetime of the
order of the age of the universe. In the latter case, their decay
products may give rise to the highest energy cosmic rays, and solve the
problem of cosmic rays beyond the GZK cutoff.
Gravitational production of particles is an important phenomenon that is
worth describing here. Consider a scalar field (particle) X of
mass MX in the expanding universe. Let
 be the
conformal time and
a(
be the
conformal time and
a(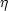 ) the
time dependence of the expansion scale factor. Assume for simplicity
that the universe is flat. The scalar field X can be expanded in
spatial Fourier modes as
) the
time dependence of the expansion scale factor. Assume for simplicity
that the universe is flat. The scalar field X can be expanded in
spatial Fourier modes as
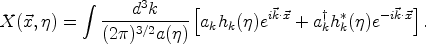 |
(34) |
Here ak and
ak† are creation and annihilation
operators, and
hk(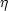 ) are mode functions that satisfy (a) the normalization
condition
hk hk'* -
h'k hk* = i
(a prime indicates a derivative with respect to conformal time),
and (b) the mode equation
) are mode functions that satisfy (a) the normalization
condition
hk hk'* -
h'k hk* = i
(a prime indicates a derivative with respect to conformal time),
and (b) the mode equation
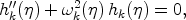 |
(35) |
where
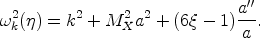 |
(36) |
The parameter 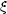 is
is
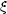 = 0 for a
minimally-coupled field and
= 0 for a
minimally-coupled field and
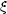 = 1/6 for a
conformally-coupled field. The mode equation, Eq. (35), is formally the
same as the equation of motion of a harmonic oscillator with
time-varying frequency
= 1/6 for a
conformally-coupled field. The mode equation, Eq. (35), is formally the
same as the equation of motion of a harmonic oscillator with
time-varying frequency
 k(
k(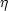 ). For a given
positive-frequency solution
hk(
). For a given
positive-frequency solution
hk(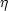 ), the vacuum
|0h> of the field X, i.e. the state with no
X particles, is defined as the state that satisfies
ak| 0h> = 0 for all k. Since
Eq. (35) is a second order equation and the frequency depends on time,
the normalization condition is in general not sufficient to specify the
positive-frequency modes uniquely, contrary to the case of constant
frequency
), the vacuum
|0h> of the field X, i.e. the state with no
X particles, is defined as the state that satisfies
ak| 0h> = 0 for all k. Since
Eq. (35) is a second order equation and the frequency depends on time,
the normalization condition is in general not sufficient to specify the
positive-frequency modes uniquely, contrary to the case of constant
frequency
 0 for which
hk0(
0 for which
hk0(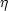 ) = e-i
) = e-i 0
0
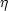 /
(2
/
(2 0)1/2. Different boundary conditions
for the solutions
hk(
0)1/2. Different boundary conditions
for the solutions
hk(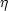 ) define in general different creation and annihilation
operators ak and
ak†, and thus in general different vacua.
4
For example, solutions which satisfy the condition of having only
positive-frequencies in the distant past,
) define in general different creation and annihilation
operators ak and
ak†, and thus in general different vacua.
4
For example, solutions which satisfy the condition of having only
positive-frequencies in the distant past,
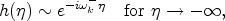 |
(37) |
contain both positive and negative frequencies in the distant future,
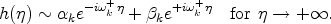 |
(38) |
Here  k± =
lim
k± =
lim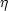
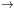 ±
±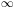
 k(
k(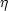 ). As a
consequence, an initial vacuum state is no longer a vacuum state at
later times, i.e. particles are created. The number density of
particles is given in terms of the Bogolubov coefficient
). As a
consequence, an initial vacuum state is no longer a vacuum state at
later times, i.e. particles are created. The number density of
particles is given in terms of the Bogolubov coefficient
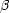 k
in Eq. (38) by
k
in Eq. (38) by
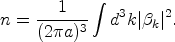 |
(39) |
These ideas have been applied to gravitational particle creation at the
end of inflation by
Chung, Kolb,
& Riotto (1998) and
Kuzmin &
Tkachev (1998).
Particles with masses MX of the order of the Hubble
parameter at the end of inflation,
HI 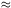 10-6 MPl
10-6 MPl
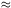 1013 GeV,
may have been created with a density which today may be comparable to
the critical density. Figure 8 shows the relic
density
1013 GeV,
may have been created with a density which today may be comparable to
the critical density. Figure 8 shows the relic
density  h2 of these WIMPZILLAs as a function of their mass
MX in units of HI. Curves are shown
for inflation models that have a smooth transition to a radiation
dominated epoch (dashed line) and a matter dominated epoch (solid
line). The third curve (dotted line) shows the thermal particle density
at temperature T = HI /
2
h2 of these WIMPZILLAs as a function of their mass
MX in units of HI. Curves are shown
for inflation models that have a smooth transition to a radiation
dominated epoch (dashed line) and a matter dominated epoch (solid
line). The third curve (dotted line) shows the thermal particle density
at temperature T = HI /
2 . Also shown in the figure is
the region where WIMPZILLAs are thermal relics. It is clear that it is
possible for dark matter to be in the form of heavy WIMPZILLAs generated
gravitationally at the end of inflation.
. Also shown in the figure is
the region where WIMPZILLAs are thermal relics. It is clear that it is
possible for dark matter to be in the form of heavy WIMPZILLAs generated
gravitationally at the end of inflation.
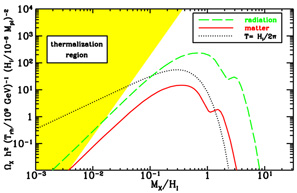 |
Figure 8. Relic density of
gravitationally-produced WIMPZILLAs as a function of their mass
MX. HI is the Hubble parameter at
the end of inflation, Trh is the reheating
temperature, and Mpl
|
2 Notice that according to the Merriam-Webster Dictionary of the English Language, a wimp is a weak, cowardly, or ineffectual person. Back.
3 We may ask if there can be points in the empty regions, or in more general terms, what is the meaning of the density of points in Figure 4, and in similar figures in Section 3. For a discussion on this, see Bergström & Gondolo (1996). Back.
4 The precise definition of a vacuum in a curved space-time is still subject to some ambiguities. We refer the interested reader to Fulling (1989); Wald (1994); Fulling (1979); Birrell & Davis (1982) and to the discussion in Chung, Notari, & Riotto (2003) and references therein. Back.