


6.2. The modern angular size test: CMB-ology
Although it is not my purpose here to discuss the CMB anisotropies,
it is necessary to say a few words on the preferred angular
scale of the longest wavelength acoustic oscillations, the "first peak",
because this is now the primary evidence for a flat Universe
( k =
0). In Fig. 4 we see again the now
very familiar plot of the angular power spectrum of anisotropies as
observed by WMAP [42]
(in my opinion, of all the WMAP papers,
this reference provides the clearest discussion of the
physics behind the peak amplitudes and positions).
The solid line is the concordance model-
not a fit, but just the predicted angular power spectrum (via CMBFAST
[41]) from the
k =
0). In Fig. 4 we see again the now
very familiar plot of the angular power spectrum of anisotropies as
observed by WMAP [42]
(in my opinion, of all the WMAP papers,
this reference provides the clearest discussion of the
physics behind the peak amplitudes and positions).
The solid line is the concordance model-
not a fit, but just the predicted angular power spectrum (via CMBFAST
[41]) from the
 m = 0.3,
m = 0.3,

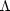 =
0.7 model Universe with an optical depth of
=
0.7 model Universe with an optical depth of

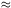 0.17 to the surface
of last scattering. I must admit that the agreement is impressive.
0.17 to the surface
of last scattering. I must admit that the agreement is impressive.
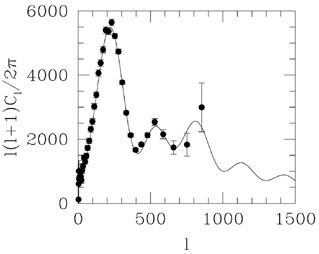 |
Figure 4. The angular power spectrum of CMB anisotropies observed by WMAP [42]. The solid line is not a fit but the is the concordance model proposed earlier [2]. |
I remind you that the harmonic index on the horizontal axis is related to angular scale as
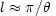 |
(6.1) |
so the first peak, at
l 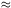 220, would
correspond to an angular scale
of about one degree. I also remind you that the first peak corresponds
to those density inhomogeneities which entered the horizon sometime before
decoupling (at z = 1000); enough before so that they have had time to
collapse to maximum compression (or expand to maximum rarefaction) just
at the moment of hydrogen recombination. Therefore, the linear scale of
these inhomogeneities is very nearly given by the sound horizon at
decoupling, that is
220, would
correspond to an angular scale
of about one degree. I also remind you that the first peak corresponds
to those density inhomogeneities which entered the horizon sometime before
decoupling (at z = 1000); enough before so that they have had time to
collapse to maximum compression (or expand to maximum rarefaction) just
at the moment of hydrogen recombination. Therefore, the linear scale of
these inhomogeneities is very nearly given by the sound horizon at
decoupling, that is
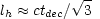 |
(6.2) |
where tdec is the age of the Universe at decoupling.
So one might say, the test is simple: we have a known linear scale
lh which corresponds to an observed angular scale
(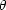
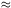 0.014 rad)
so we can determine the geometry of the Universe. It is not quite so
simple because the linear scale, lh depends, via
tdec on the matter content of the Universe
(
0.014 rad)
so we can determine the geometry of the Universe. It is not quite so
simple because the linear scale, lh depends, via
tdec on the matter content of the Universe
( m);
basically, the
larger
m);
basically, the
larger  m,
the sooner matter dominates the expansion, and the earlier
decoupling with a correspondingly smaller lh. This
comoving linear scale is shown in
Fig. 5 as a function of
m,
the sooner matter dominates the expansion, and the earlier
decoupling with a correspondingly smaller lh. This
comoving linear scale is shown in
Fig. 5 as a function of
 m
(
m
(
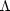 hardly
matters here, because the vacuum energy density which dominates today has
no effect at the epoch of decoupling). Another complication is that
the angular size distance to the surface of last scattering not only
depends upon the geometry, but also upon the expansion history. This is
evident in Fig. 6 which shows the comoving
angular size distance (in Gpc) to the surface of last scattering as a
function of
hardly
matters here, because the vacuum energy density which dominates today has
no effect at the epoch of decoupling). Another complication is that
the angular size distance to the surface of last scattering not only
depends upon the geometry, but also upon the expansion history. This is
evident in Fig. 6 which shows the comoving
angular size distance (in Gpc) to the surface of last scattering as a
function of
 m for three
values of
m for three
values of
 tot =
tot =
 m +
m +

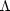 (i.e.,
(i.e.,
 k = 1 -
k = 1 -
 tot).
Note that the comoving angular size distance, DA(1 +
z), is the same as the radial comoving coordinate r.
tot).
Note that the comoving angular size distance, DA(1 +
z), is the same as the radial comoving coordinate r.
 |
Figure 5. The comoving linear scale of the
perturbation corresponding to the first peak as a function of
|
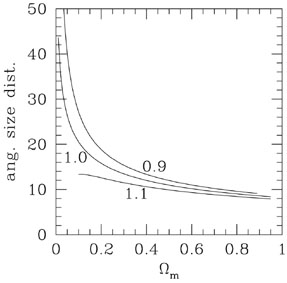 |
Figure 6. The angular size distance (Gpc)
to the last scattering surface (z = 1000) as a function of
|
We can combine Figs. 5 and
6 to plot
the expected angular size (or harmonic index) of the first peak as
a function of
 m and
m and
 tot, and
this is shown in
Fig. 7 with the dashed line giving the observed
l of the first peak. We see that a model with
tot, and
this is shown in
Fig. 7 with the dashed line giving the observed
l of the first peak. We see that a model with
 tot
tot
 1.1 (a closed universe) is
clearly ruled out, but it would be possible to have an open model with
1.1 (a closed universe) is
clearly ruled out, but it would be possible to have an open model with
 tot = 0.9
and
tot = 0.9
and  m = 0.8
from the position of the first
peak alone; the predicted peak amplitude, however, would be about
40% too low. The bottom line of all of this is that the position
of the first peak does not uniquely define the geometry of the Universe
because of a degeneracy with
m = 0.8
from the position of the first
peak alone; the predicted peak amplitude, however, would be about
40% too low. The bottom line of all of this is that the position
of the first peak does not uniquely define the geometry of the Universe
because of a degeneracy with
 m (I
haven't mentioned the degeneracy with h taken here to be 0.72).
To determine whether or not we live in a flat Universe we need an
independent handle on
m (I
haven't mentioned the degeneracy with h taken here to be 0.72).
To determine whether or not we live in a flat Universe we need an
independent handle on
 m and
that is provided, in WMAP data, by
the amplitudes of the first two peaks (the more non-baryonic matter, the
deeper the forming potential wells, and the lower the amplitudes).
From this it is found that
m and
that is provided, in WMAP data, by
the amplitudes of the first two peaks (the more non-baryonic matter, the
deeper the forming potential wells, and the lower the amplitudes).
From this it is found that
 m
m
 0.3, and from
Fig. 7 we see
that the model Universe should be near flat
(
0.3, and from
Fig. 7 we see
that the model Universe should be near flat
( tot
tot
 1.0).
Of course if the Universe is near flat with
1.0).
Of course if the Universe is near flat with
 m = 0.3
then the rest must be in dark energy; this is the indirect evidence from
the CMB anisotropies for dark energy.
m = 0.3
then the rest must be in dark energy; this is the indirect evidence from
the CMB anisotropies for dark energy.
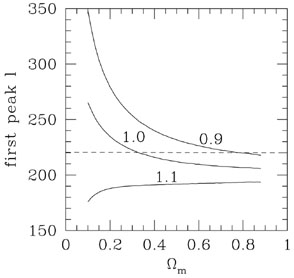 |
Figure 7. The harmonic index expected for
the first peak as a function
of |
I just add here that the observed peak amplitudes (given the optical depth to z = 1000 determined from WMAP polarization results [43]), is taken now as definitive evidence for CDM. However, alternative physics which affects the amplitude and positions of peaks (e.g. [3] could weaken this conclusion, as well as affect the derived cosmological parameters. Even taking the peak amplitudes as prima facie evidence for the existence of cold dark matter, it is only evidence for CDM at the epoch of recombination (z = 1000) and not in the present Universe. To address the cosmic coincidence problem, models have been suggested in which dark matter transmutes into dark energy (e.g. [44]).
Now I turn to the direct evidence for dark energy.