


4.1. Parametrized equation of state and cosmological observations
One simple, phenomenological, procedure for comparing observations with theory is to parameterize the function w(a) in some suitable form and determine a finite set of parameters in this function using the observations. Theoretical models can then be reduced to a finite set of parameters which can be determined by this procedure. To illustrate this approach, and the difficulties in determining the equation of state of dark energy from the observations, we shall assume that w(a) is given by the simple form: w(a) = w0 + w1(1 - a); in the k = 0 model (which we shall assume for simplicity), w0 measures the current value of the parameter and - w1 gives its rate of change at the present epoch. In addition to simplicity, this parameterization has the advantage of giving finite w in the entire range 0 < a < 1.
Figure 12 shows confidence interval contours in
the w0 - w1 plane arising from
the full supernova data, obtained by assuming that
 NR +
NR +

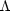 = 1. The three
frames are for
= 1. The three
frames are for
 NR =
(0.2, 0.3, 0.4). The following features are
obvious from the figure: (i) The cosmological constant corresponding to
w0 = - 1, w1 = 0
is a viable candidate and cannot be excluded. (In fact, different
analysis of many observational results lead to this conclusion
consistently; in other words, at present there is no observational
motivation to assume w1
NR =
(0.2, 0.3, 0.4). The following features are
obvious from the figure: (i) The cosmological constant corresponding to
w0 = - 1, w1 = 0
is a viable candidate and cannot be excluded. (In fact, different
analysis of many observational results lead to this conclusion
consistently; in other words, at present there is no observational
motivation to assume w1
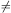 0.) (ii) The result is
sensitive to the value of
0.) (ii) The result is
sensitive to the value of
 NR which
is assumed. This is understandable from equation (44) which shows that
wX(a) depends on both
Q
NR which
is assumed. This is understandable from equation (44) which shows that
wX(a) depends on both
Q 
 NR and
H(a). (We shall discuss this dependence of the results on
NR and
H(a). (We shall discuss this dependence of the results on
 NR in
greater detail below). (iii) Note that the axes are not in equal units
in figure 12. The observations can determine
w0 with far greater accuracy than w1. (iv) The
slanted line again corresponds to
H0dL(z = 0.63) = constant and
shows that the shape of the probability ellipses arises essentially from
this feature.
NR in
greater detail below). (iii) Note that the axes are not in equal units
in figure 12. The observations can determine
w0 with far greater accuracy than w1. (iv) The
slanted line again corresponds to
H0dL(z = 0.63) = constant and
shows that the shape of the probability ellipses arises essentially from
this feature.
In summary, the current data definitely supports a negative pressure component with w0 < - (1/3) but is completely consistent with w1 = 0. If this is the case, then the cosmological constant is the simplest candidate for this negative pressure component and there is very little observational motivation to study other models with varying w(a). On the other hand, the cosmological constant has well known theoretical problems which could possibly be alleviated in more sophisticated models with varying w(a). With this motivation, there has been extensive amount of work in the last few years investigating whether improvement in the observational scenario will allow us to determine whether w1 is non zero or not. (For a sample of references, see [110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125].) In the context of supernova based determination of dL, it is possible to analyze the situation along the following lines [79].
Since the supernova observations essentially measure dL(a), accuracy in the determination of w0 and w1 from (both the present and planned future [126]) supernova observations will crucially depend on how sensitive dL is to the changes in w0 and w1. A good measure of the sensitivity is provided by the two parameters
 |
(45) |
Since dL(z, w0,
w1) can be obtained from theory, the
parameters A and B can be computed form theory in a straight
forward manner. At any given redshift z, we can plot contours of
constant A and B in the w0 -
w1 plane.
Figure (13) shows the result of such an
analysis
[79].
The two frames on the left are at z = 1 and the two frames on
the right are at z = 3. The top frames give contours of constant
A and bottom frame give contours of constant B.
From the definition in the equation (45) it is clear that A and
B can be interpreted as the fractional change in
dL for unit change
in w0, w1. For example, along the
line marked A = 0.2 (in the top left frame) dL
will change by 20 per cent for unit change in w0. It
is clear from the two top frames that for most of the
interesting region in the w0 - w1
plane, changing w0 by
unity changes dL by about 10 per cent or
more. Comparison of
z = 1 and z = 3 (the two top frames) shows that
the sensitivity is higher at high redshift, as to be expected.
The shaded band across the picture corresponds to the region
in which -1 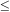 w(a)
w(a)
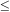 0 which is of primary
interest in constraining dark energy with negative pressure.
One concludes that determining w0 from
dL fairly accurately will not be too daunting a task.
0 which is of primary
interest in constraining dark energy with negative pressure.
One concludes that determining w0 from
dL fairly accurately will not be too daunting a task.
The situation, however, is quite different as regards w1 as illustrated in the bottom two frames. For the same region of the w0 - w1 plane, dL changes only by a few percent when w1 changes by unity. That is, dL is much less sensitive to w1 than to w0. It is going to be significantly more difficult to determine a value for w1 from observations of dL in the near future. Comparison of z = 1 and z = 3 again shows that the sensitivity is somewhat better at high redshifts but only marginally.
The situation is made worse by the fact that dL also
depends on the parameter
 NR. If
varying
NR. If
varying  NR
mimics the variation of w1 or w0,
then, one also needs to determine the sensitivity of
dL to
NR
mimics the variation of w1 or w0,
then, one also needs to determine the sensitivity of
dL to
 NR.
Figure 14 shows contours of constant
H0 dL in the
NR.
Figure 14 shows contours of constant
H0 dL in the
 NR -
w0 and
NR -
w0 and
 NR -
w1
planes at two redshifts z = 1 and z = 3. The two top
frames shows that if one varies the value of
NR -
w1
planes at two redshifts z = 1 and z = 3. The two top
frames shows that if one varies the value of
 NR in the
allowed range of, say, (0.2, 0.4) one can move along
the curve of constant dL and induce fairly large
variation in w1. In other words, large changes in
w1 can be easily compensated by small changes in
NR in the
allowed range of, say, (0.2, 0.4) one can move along
the curve of constant dL and induce fairly large
variation in w1. In other words, large changes in
w1 can be easily compensated by small changes in
 NR
while maintaining the same value for dL at a given
redshift. This shows that the uncertainty in
NR
while maintaining the same value for dL at a given
redshift. This shows that the uncertainty in
 NR introduces
further difficulties in determining w1 accurately from
measurements of dL. The two lower frames show that
the situation is better as regards w0. The curves are much
less steep and hence varying
NR introduces
further difficulties in determining w1 accurately from
measurements of dL. The two lower frames show that
the situation is better as regards w0. The curves are much
less steep and hence varying
 NR does not
induce large variations in w0. We are once again
led to the conclusion that unambiguous determination of
w1 from data will be quite difficult. This is
somewhat disturbing since w1
NR does not
induce large variations in w0. We are once again
led to the conclusion that unambiguous determination of
w1 from data will be quite difficult. This is
somewhat disturbing since w1
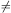 0 is a clear
indication of a dark energy component which is evolving.
It appears that observations may not be of great help
in ruling out cosmological constant as the major dark energy
component. (The results given above are based on
[79];
also see
[127]
and references cited therein.)
0 is a clear
indication of a dark energy component which is evolving.
It appears that observations may not be of great help
in ruling out cosmological constant as the major dark energy
component. (The results given above are based on
[79];
also see
[127]
and references cited therein.)