Annu. Rev. Astron. Astrophys. 1994. 32: 153-90 Copyright © 1994 by Annual Reviews. All rights reserved

2. GENERAL CONSIDERATIONS

The Master said, "Ssu, I believe you look upon me as one whose aim is simply to learn and retain in mind as many things as possible." He replied, "That is what I thought. Is it not so?" The Master said, "No; I have one thread on which I string them all:"

The Analects of Confucius

The r-, s-, and p-processes are distinct nucleosynthetic mechanisms. They occur in different environments and under quite different conditions. Nevertheless, it is useful to seek some unifying concept by which we may understand these disparate processes. We will see that entropy is the concept we need. Careful consideration of entropy in the various nucleosynthetic processes will clarify our discussion and give us insight into how these processes occur and why they occur where they do. With this insight we will see how the r-, s-, and p-processes are each unique answers to the same question: "How does nature produce heavy elements?"

2.1. Entropy and Equilibrium

Let us begin our discussion by considering a given thermally isolated system at constant volume. The system has total energy E₀. The entropy of this system is

(1)

where k is Boltzmann's constant and 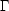is the number of energetically allowed macroscopic states available to the system. By macroscopic state we mean a particular distribution of the constituents of the system among their single- particle quantum-mechanical states. In essence, a macroscopic state of the system is one particular way the constituents of the system can share the total energy E₀. Suppose the system does not have all macroscopic states of energy E₀ available to it. In this case, the entropy is less than its maximum. The system will evolve by the Second Law of Thermodynamics and add more macroscopic states to its repertoire. In this evolution, the entropy will thus increase. The system will continue to evolve until all macroscopic states of energy E₀ are available to the system. Once the system reaches this point, it is at maximum entropy and experiences no further evolution. The system has attained equilibrium. We thus see that equilibrium, or maximum entropy, is the evolutionary endpoint of any thermally isolated system.

We can now use these considerations to ask what happens to the nucleons and nuclei in some nucleosynthetic environment. If the system of nucleons and nuclei is thermally isolated and out of equilibrium, it will evolve towards equilibrium. Given enough time, the system will reach equilibrium and attain maximum entropy. At this point, it is in nuclear statistical equilibrium (NSE), and it is a simple matter to compute the abundance of any nuclide (Burbidge et al 1957). We find (e.g. Meyer 1993) that, for a nuclear species of atomic number Z and mass number A, the abundance per baryon Y(Z, A) is

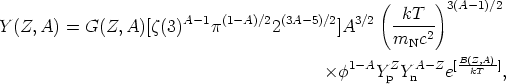
(2)

where G(Z, A) is the nuclear partition function, 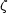(3) is the Riemann zeta function of argument 3, T is the temperature, m_N is the mass of a single baryon, 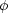is the photon-to-baryon ratio, Y_p, is the abundance per baryon of protons, Y_n is the abundance per baryon of neutrons, and B(Z, A) is the binding energy of nucleus (Z, A). We note that 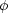is given by

(3)

where 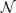_A is Avagadro's number and p is the baryon mass density. The binding energy of nucleus (Z, A) is

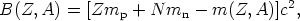
(4)

where N = A - Z and m(Z, A), m_p, and m_n are the masses of nucleus (Z, A), the proton, and the neutron, respectively.

From Equation (2), we see that the NSE abundance of nuclei is nonzero. This might at first be surprising. If we combine free neutrons and protons into nuclei, we decrease the number of free particles of the system. This would yield fewer ways of sharing the total energy of the system and thus decrease the number of macroscopic states available to the system. The nuclear reactions also release binding energy, however, which increases the number of photons in the system, the energy available to leptons, and the excitation energy in the nuclei. These effects increase the number of ways the system can share the total energy of the system and, hence, can increase the number of macroscopic states available to the system. This increase can more than compensate for the decrease in the number of states due to the loss of free particles and can lead to an increase in the entropy. Once the system has evolved to the point that it experiences no net increase in the number of macroscopic states by changing the abundance of any particular nucleus, the system has reached NSE.

Which nuclei dominate the abundance distribution in NSE? This depends on the photon-to-baryon ratio or, equivalently, the entropy per baryon since this latter quantity scales monotonically with the photon-to-baryon ratio (e.g. Meyer & Walsh 1993). From Equation (2) we see that the abundance of some heavy nucleus (Z, A) depends on ^1-A. At some given temperature then, the larger 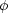is, the smaller will be the abundance of the heavy nucleus (Z, A). Fewer heavy nuclei means more light nuclei and free nucleons. The strong dependence of the NSE abundances on 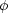will be crucial for the r-process. This dependence on 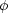is apparent in Figure 2. If we fix the temperature, the larger 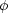is, the more likely nucleons are free or contained in light nuclei.

Figure 2. The dominant species in NSE for a gas with electron-to-Baryon ratio Ye = 0.5. The different regions of the plot show at what temperatures and photon-to-baryon ratios the various species dominate the gas. At high temperatures and high photon-to-baryon ratios, free neutrons and protons (labeled n, p) dominate. At lower temperatures and photon-to-baryon ratios, the nucleons are mostly locked up in 4He nuclei. At still lower temperatures and photon-to-baryon ratios, the gas will predominantly be a distribution of iron-group nuclei.