3.2.2 Horizons

Schwarzschild (1916) derived a special solution to the original Einstein equations. The Schwarzschild metric has the line element

with 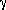= 1 - (2m / r).

Eddington (1924) showed that the introduction of the cosmological constant led to an extended factor

in the line element and thus to a second horizon, the `world horizon'.

Different usage of the term horizon made standardization desirable. It was provided by Rindler (1956).

``We shall define a horizon as a frontier between things observable and things unobservable. (The vague term thing is here used deliberately). There are then two quite different horizon concepts in cosmology which satisfy our definition and to which cosmologists have at different times devoted their attention. The first, which I shall call an event-horizon, is exemplified by the de Sitter model-universe. It may be defined as follows: An event-horizon, for a given fundamental observer A, is a (hyper-) surface in space-time which divides all events into two non-empty classes: those that have been, are or will be observable by A, and those that are forever outside A's Possible Powers of observation . . . .

The other type of horizon, which I shall call a particle-horizon ⁽⁸⁾, is exemplified by the Einstein-de Sitter model-universe. It may be defined as follows: A particle-horizon, for any given fundamental observer A and cosmic instant t₀ is a surface in the instantaneous 3-space t = t₀ to, which divides all fundamental particles into two non-empty classes: Those that have already been observable by A at time t₀ and those that have not.''

Fig. 27 gives an illustration of horizons.

Figure 27. Light-paths in a model-universe (similar to a Friedmann-Lemaitre model) possessing both a particle horizon and an event-horizon (Rindler 1956): ``The origin-observer is denoted by A. B is an observer on a typical particle which becomes visible to A at creation-time t1 (when A and B enter each other's creation-light-cones) and which passes beyond A's event-horizon at time t2, so that events at B after t2 are outside A's possible powers of observation. C is the critical particle which becomes visible to A only at t = . C's creation-light-track towards A is that of the unique photon which reaches A at t = , and which we have already identified with A's event-horizon. And in the same way that A approaches asymptotically the boundary of C's creation-light-cone, so C approaches that of A's creation-light-cone. Evidently all particles beyond C are entirely outside A's cognizance. In the diagram only the positions near the vertices of the creation-light-cones have been shaded in. We may note that the existence of a critical particle with properties analogous to those of C above, one on each line of vision of each fundamental observer, is a general feature of all models possessing both types of horizon.''