© CAMBRIDGE UNIVERSITY PRESS 1999

1.7.6 Advantages of Mixed CHDM Over Pure CDM Models

There are three basic reasons why a mixture of cold plus hot dark matter works better than pure CDM without any hot particles: (1) the power spectrum shape P (k) is a better fit to observations, (2) there are indications from observations for a more weakly clustering component of dark matter, and (3) a hot component may help avoid the too-dense central dark matter density in pure CDM dark matter halos. Each will be discussed in turn.

(1) Spectrum shape. As explained in discussing WDM vs. CHDM above, the pure CDM spectrum P (k) does not fall fast enough on the large-k side of its peak in order to fit indications from galaxy and cluster correlations and power spectra. The discussion there of ``Excess Power'' is a way of quantifying this. This is also related to the overproduction of clusters in pure CDM. The obvious way to prevent = 1 SCDM normalized to COBE from overproducing clusters is to tilt it a lot (the precise amount depending on how much of the COBE fluctuations are attributed to gravity waves, which can be increasingly important as the tilt is increased). But a constraint on CDM-type models that is likely to follow both from the high-z data just discussed and from the preliminary indications on cosmic microwave anisotropies at and beyond the first acoustic peak from the Saskatoon experiment (Netterfield et al. 1997) is that viable models cannot have much tilt, since that would reduce too much both their small-scale power and the amount of small-angle CMB anisotropy. As already explained, by reducing the fluctuation power on cluster scales and below, COBE-normalized CHDM naturally fits both the CMB data and the cluster abundance without requiring much tilt. The need for tilt is further reduced if a high baryon fraction _b 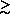0.1 is assumed (M. White et al. 1996), and this also boosts the predicted height of the first acoustic peak. No tilt is necessary for 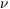= 0.2 shared between N 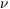= 2 neutrino species with h = 0.5 and _b = 0.1. Increasing the Hubble parameter in COBE-normalized models increases the amount of small-scale power, so that if we raise the Hubble parameter to h = 0.6 keeping 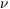= 0.2 and _b = 0.1(0.5/h)² = 0.069, then fitting the cluster abundance in this N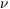 = 2 model requires tilt 1 - n_p 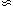0.1 with no gravity waves (i.e., T/S = 0; alternatively if T/S = 7(1 - n_p) is assumed, about half as much tilt is needed, but the observational consequences are mostly very similar, with a little more small scale power). The fit to the small-angle CMB data is still good, and the predicted _gas in damped Lyman systems is a little higher than for the h = 0.5 case. The only obvious problem with h = 0.6 applies to any = 1 model - the universe is rather young: t₀ = 10.8 Gyr. But the revision of the globular cluster ages with the new Hipparcos data may permit this.

(2) Need for a less-clustered component of dark matter. The fact that group and cluster mass estimates on scales of ~ 1 h^-1 Mpc typically give values for around 0.1-0.2 while larger-scale estimates give larger values around 0.3-1 (Dekel 1994) suggests that there is a component of dark matter that does not cluster on small scales as efficiently as cold dark matter is expected to do. In order to quantify this, the usual group M/L measurement of ₀ on small scales has been performed in ``observed'' = 1 simulations of both CDM and CHDM (Nolthenius, Klypin, & Primack 1997). We found that COBE-normalized 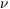= 0.3 CHDM gives _M/L = 0.12-0.18 compared to _M/L = 0.15 for the CfA1 catalog analyzed exactly the same way, while for CDM _M/L = 0.34-0.37, with the lower value corresponding to bias b = 1.5 and the higher value to b = 1 (still below the COBE normalization). Thus local measurements of the density in = 1 simulations can give low values, but it helps to have a hot component to get values as low as observations indicate. We found that there are three reasons why this virial estimate of the mass in groups misses so much of the matter in the simulations: (1) only the mass within the mean harmonic radius r_h is measured by the virial estimate, but the dark matter halos of groups continue their roughly isothermal falloff to at least 2r_h, increasing the total mass by about a factor of 3 in the CHDM simulations; (2) the velocities of the galaxies are biased by about 70% compared to the dark matter particles, which means that the true mass is higher by about another factor of 2; and (3) the groups typically lie along filaments and are significantly elongated, so the spherical virial estimator misses perhaps 30% of the mass for this reason. Visualizations of these simulations (Brodbeck et al. 1997) show clearly how extended the hot dark matter halos are. An analysis of clusters in CHDM found similar effects, and suggested that observations of the velocity distributions of galaxies around clusters might be able to discriminate between pure cold and mixed cold + hot models (Kofman et al. 1996). This is an area where more work needs to be done - but it will not be easy since it will probably be necessary to include stellar and supernova feedback in identifying galaxies in simulations, and to account properly for foreground and background galaxies in observations.

(3) Preventing too dense centers of dark matter halos. Flores and Primack (1994) pointed out that dark matter density profiles with 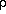(r) 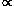r^-1 near the origin from high-resolution dissipationless CDM simulations (Dubinski & Carlberg 1991; Warren et al. 1992; Crone, Evrard, & Richstone 1994) are in serious conflict with data on dwarf spiral galaxies (cf. Moore 1994), and in possible conflict with data on larger spirals (Flores et al. 1993) and on clusters (cf. Miralda-Escudé 1995, Flores & Primack 1996). Navarro, Frenk, & White (1996; cf. Cole & Lacey 1996) agree that rotation curves of small spiral galaxies such as DDO154 and DDO170 are strongly inconsistent with their universal dark matter profile 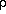_NFW(r) 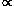1 / [r(r + a)²]. Navarro, Eke, & Frenk (1996) proposed a possible explanation for the discrepancy regarding dwarf spiral galaxies involving slow accretion followed by explosive ejection of baryonic matter from their cores, but it is implausible that such a process could be consistent with the observed regularities in dwarf spirals (Burkert 1995); in any case it will not work for low-surface-brightness galaxies. Work is in progress with Stephane Courteau, Sandra Faber, Ricardo Flores, and others to see whether the 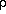_NFW universal profile is consistent with data from high- and low-surface-brightness galaxies with moderate to large circular velocities, and with Klypin, Kravtsov, and Bullock to see whether higher resolution simulations for a wider variety of models continue to give _NFW. The failure of earlier simulations to form cores as observed in dwarf spiral galaxies either is a clue to a property of dark matter that is not understood, or is telling us that the simulations were inadequate. It is important to discover whether this is a serious problem, and whether inclusion of hot dark matter or of dissipation in the baryonic component of galaxies can resolve it. It is clear that including hot dark matter will decrease the central density of dark matter halos, both because the lower fluctuation power on small scales in such models will prevent the early collapse that produces the highest dark matter densities, and also because the hot particles cannot reach high densities because of the phase space constraint (Tremaine & Gunn 1979, Kofman et al. 1996). But this may not be necessary, or alternatively it may not be enough.