© CAMBRIDGE UNIVERSITY PRESS 1999

3.5 The Anthropic Principle

Our discussion of cosmology so far has leaned heavily on the Copernican principle that we are not privileged observers of the universe. However, there are some aspects of the subject for which this principle has to be discarded; as in quantum mechanics, we have to ask whether the mere presence of an observer influences the system under study. At first sight, it may seem absurd to think of humanity influencing in any way the global properties of the universe, but the simple fact of our existence does turn out to have profound consequences. These ideas are given the label ``anthropic'', and we speak of the anthropic principle when discussing the universe in the context of the existence of observers. However, this is an area that generates controversy, and not everyone will agree on the degree of importance of anthropic ideas. See Barrow & Tipler (1986) for a thorough review of the subject. Like religious schisms, the anthropic dogma comes in varying forms and degrees of elaboration. We can distinguish perhaps three sets of attitudes to anthropic reasoning: trivial, weak and strong anthropic principles.

THE TRIVIAL ANTHROPIC PRINCIPLE 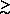This is not strictly part of the anthropic principle proper, but consists of anthropic ideas on which almost everyone can agree - i.e. that we can use observations of humanity as cosmological information in the same way as we use data from telescopes. For example, we can deduce that the universe is 1 Gyr old merely by noting that carbon-based life has formed, and that there needed to be time for typical stars to go through their life cycle and distribute heavy elements in order for this to have happened. The existence of humanity thus gives us a bound on H₀. That is about as far as such trivial anthropic arguments go in cosmology; they are in a sense unnecessary, as we have direct dating of the Earth to set a much more precise limit on H₀, a constraint that was astronomically important in the early days of the distance scale, when values of H₀ 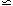500 km s^-1 were suggested.

However, anthropic arguments of this type have an honourable history from the 19th century, when the Earth could not be dated directly. At that time, Lord Kelvin was advocating an age for the Earth of only ~ 10⁷ years, based on its cooling time. Evolutionary biologists were able to argue that this was an inadequate time to allow the development of species, a conclusion that was vindicated by the discovery of radioactivity (which allowed both the dating of the Earth and showed the flaw in Kelvin's argument). Here was an excellent example of important astronomical conclusions being drawn from observations of life on Earth.

THE WEAK ANTHROPIC PRINCIPLE Moving on from the astronomical consequences of humanity's observations of their planet, are there cosmological inferences to be drawn from the existence of humanity itself? This question arises because the very possibility of carbon-based life seems to depend on a series of striking coincidences, as first pointed out in a seminal article by Dicke (1961).

The most striking of Dicke's arguments is based upon the mechanism for the production of the elements. As we shall see, it is now thought virtually certain that the abundances of the light elements up to ⁷Li were determined by the progress of nuclear reactions in the early stages of the big bang. Heavier elements were produced at a much later stage by fusion in stars. Incidentally, this division of labour represents an ironic end to a historically important debate concerning the origin of the universe, which dominated cosmology in the 1960s. The epochal paper that became universally known just as B²FH (Burbidge, Burbidge, Fowler & Hoyle 1957) was concerned with showing how the elements could be built up by nuclear reactions in stars. Although this was not the motivation for the work, these mechanisms provided a vital defence for the steady-state model (which never passes through a hot phase) against the belief of Gamow and coworkers that all elements could be synthesized in the big bang (Gamow 1946; Alpher, Bethe & Gamow 1948). Although the steady-state model passed away, the arguments of B²FH have become part of current orthodoxy, leaving only the lightest elements adhering to Gamow's vision.

Now, the fascinating aspect of all this is that synthesis of the higher elements is rather hard, owing to the non-existence of stable elements with atomic weights A = 5 or A = 8. This makes it hard to build up heavy nuclei by collisions of ¹H, ²D, ³He and ⁴He nuclei. The only reason that heavier elements are produced at all is the reaction

(3.98)

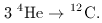
A three-body process like this will only proceed at a reasonable rate if the cross-section for the process is resonant: i.e. if there is an excited energy level of the carbon nucleus that matches the typical energy of three alpha particles in a stellar interior. The lack of such a level would lead to negligible production of heavy elements - and no carbon-based life. Using these arguments, Hoyle made a breathtaking leap of the imagination to predict that carbon would display such a resonance, which was duly found to be the case (Hoyle et al. 1953).

In a sense, this is just trivial anthropic reasoning: we see carbon on Earth, and nuclear physics gives us an inevitable conclusion to draw. And yet, one is struck by the coincidence: if the energy levels of carbon had been only slightly different, then it is reasonable to assume that the development of life anywhere in the universe would never have occurred. Does this mean that some controlling agent designed nuclear physics specifically to produce life? Perhaps, but it is not so easy to prove one way or the other, as we can see from the following arguments.

Suppose we imagine some process that produces an ensemble of a large number of universes with widely varying properties or even physical laws. What the weak anthropic principle points out is that only those members of the ensemble that are constructed so as to admit the production of intelligent life at some stage in their evolution will ever be the subject of cosmological enquiry. The fact that we are observers means that, if the production of life is at all a rare event, any universe that we can see is virtually guaranteed to display bizarre and apparently improbable coincidences. The ¹²C energy level is one such; another goes under the heading of Dirac's large-number hypothesis. Dirac noted that very large dimensionless numbers often arise in both particle physics and cosmology. The ratio of the electrostatic and gravitational forces experienced by an electron in a hydrogen atom is

(3.99)

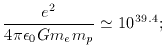
one of the problems of unifying gravity and other forces is understanding how such a vast dimensionless number can be generated naturally. In a cosmological context, the weakness of gravity manifests itself in the fact that the Hubble radius is enormously greater than the Planck length:

(3.100)

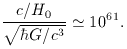
This number is very nearly the 1.5 power of the previous large number: it is as if these large numbers were quantized in steps of 10²⁰. Dirac proposed that the coincidence must indicate a causal relation; requiring the proportionality to hold at all times then yields the radical consequence

(3.101)

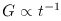
(because H₀ declines as ~ t^-1 as the universe ages).

Geological evidence shows that this prediction is not upheld in practice, since the sun would have been hotter in the past. A less radical explanation of the large-number coincidence uses the anthropic idea that life presumably requires the existence of elements other than hydrogen and helium. The universe must therefore be old enough to allow typical stars to go through their life cycle and produce ``metals''. This condition can be expressed in terms of fundamental constants as follows. Stars have masses of the order of the Chandrasekhar mass

(3.102)

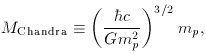
where m_p is the proton mass (see chapter 2). The luminosity of a star dominated by electron-scattering opacity is [problem 5.1]

(3.103)

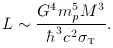
The characteristic lifetime of a star, M_Chandra c² / L, can thus also be expressed in fundamental constants, and is

(3.104)

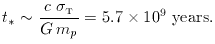
Comparing with the above, we see that the large-number coincidence is just t_* ~ H₀^-1; i.e. the universe must be old enough for the stars to age. The fact that the universe is not very much older than this may tell us that we are privileged to be in the first generation of intelligence to arise after the big bang: civilizations arising in >> 10¹⁰ years time will probably not spend their time in cosmological enquiry, as they will be in contact with experienced older races who know the answers already. Lastly, the coincidence can be used to argue for the fundamental correctness of the big bang as against competitors such as the steady-state theory; if the universe is in reality very much older than t_*, there is no explanation for the coincidence between t_* and H₀^-1.

In short, the weak anthropic principle states that, because intelligent life is necessary for cosmological enquiry to take place, this already imposes strong selection effects on cosmological observations. Note that, despite the name, there is no requirement for the life to be human, or even carbon based. All we say is that certain conditions can be ruled out if they do not lead to observers, and this is one of the weaknesses of the principle: are we really sure that life based on elements less massive than carbon is impossible? The whole point of these arguments is that it only has to happen once.

It is nevertheless at least plausible that the ``anthropic'' term may not be a complete misnomer. It has been argued (see Carter 1983) that intelligent life is intrinsically an extremely unlikely phenomenon, where the mean time for development could be very long:

(3.105)

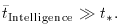
If the inequality was sufficiently great, it would be surprising to find even one intelligent system within the current horizon. The anthropic principle provides a means for understanding why the number is non-zero, even when the expectation is small, but there would be no reason to expect a second system; humanity would then probably be alone in the universe. On the other hand, 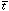_Intelligence may be shorter, and then other intelligences would be common. Either possibility is equally consistent with the selection effect imposed by our existence, although the fact that life on Earth took billions of years to develop is consistent with the former view; if life is a rare event, it would not appear early in the allowed span of time.

OTHER WEAK ANTHROPIC DEDUCTIONS What other features of the universe might be amenable to anthropic arguments? The striking aspects to explain are that we live in a universe with roughly critical density in matter, dominating a radiation background of 2.73 K by roughly four powers of 10. Our starting point is the age argument given above, plus the assumption that life will only arise (a) after recombination (so that we are not cooked); (b) after matter domination (so that matter can self-gravitate into stars):

(3.106)

A first coincidence to consider is that recombination and matter-radiation equality occur at relatively similar times; why is this? Recombination requires a temperature of roughly the ionization potential of hydrogen:

(3.107)

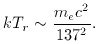
The mass ratio of baryons and photons at recombination is therefore 137² m_p / m_e ~ 10^7.5, and the universe will be matter dominated at recombination unless the ratio of photon and proton number densities exceeds this value. At high temperatures, kT > m_p c², baryon, antibaryon and photon numbers will be comparable; it is thought that the present situation arises from a particle-physics asymmetry between matter and antimatter, so that baryons and antibaryons do not annihilate perfectly (see chapter 9). Matter-radiation equality thus arises anywhere after a redshift 10^7.5 times larger than that of last scattering, and could be infinitely delayed if the matter/antimatter asymmetry were small enough. The approximate coincidence in epochs says that the size of the particle/antiparticle asymmetry is indeed roughly 137² m_p / m_e, and it is not implausible that such a relation might arise from a complete particle physics model. At any rate, it seems to have no bearing on anthropic issues.

The anthropic argument for the age of the universe lets us work out the time of recombination, if we accept for the moment that ~ 1 (see below). The age for an Einstein-de Sitter model would tell us both H₀ & ₀, and hence the current number density of photons, if we could obtain the photon-to-baryon ratio from fundamental arguments. Since n T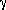³, that would give the present photon temperature, and hence the redshift of recombination. The fact that this was relatively recent (only at z ~ 10³ reflects the fact that the photon-to-baryon ratio is ~ 10⁷ rather than a much larger number.

Finally, what do anthropic arguments have to say about the cosmic density parameter, ? We have already mentioned the instability in :

(3.108)

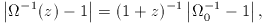
so that (z) has to be fine-tuned at early epochs to achieve 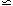1 now. We can go some way towards explaining this by appealing to some results that will be proved in later chapters. The formation of galaxies can only occur at a redshift z_f such that (z_f) ~ 1, otherwise growth of density perturbations switches off; ₀ must be unity to within a factor ~ (1 + z_f). The redshift z_f must occur after matter-radiation equality, otherwise radiation pressure would prevent galaxy-scale systems from collapsing. Any universe with >> 10^-3 at t = t_* would then have great difficulty in generating the nonlinear systems needed for life. Similar arguments can be made concerning the contribution of a cosmological constant to (Weinberg 1989; Efstathiou 1995): structures cannot form after the time at which the universe becomes dominated by any cosmological term. On the other hand, because formation is constrained to occur between a redshift of order unity and 10³, the vacuum density could presently exceed the density in matter by a factor of up to 10⁹ without preventing structure formation. There is no anthropic reason for it to be any smaller.

These arguments are impressive, but frustratingly limited. Although a rough allowed area of parameter space can be delineated, proper physical mechanisms are required to explain why a particular point in the parameter space was selected by reality. Given such a mechanism, why do we need anthropic reasoning at all? Worse still, anthropic reasoning tends to predict a universe at the extremes of the allowed range. Consider a generator of an ensemble of universes creating them with various values of (t_*). Owing to the fine-tuning required, we expect that the probability of a given result is a strongly increasing function of | - 1|. Multiply this by a probability of generating intelligence that declines with | - 1| slowly at first, and we should expect a life-selected universe to have a peak probability near to the very largest or smallest possible values of | - 1|. This is not the observed situation: anthropic arguments may therefore not be relevant to determining , even if their importance in explaining the large-number ratios cannot be challenged.

THE STRONG ANTHROPIC PRINCIPLE The ultimate form of anthropic reasoning is to assert that the coincidences we have remarked on are more than that: that the universe must be such as to admit the production of intelligent life at some time. This idea is known as the strong anthropic principle. Is such an idea a part of testable science? The whole basis of the weak anthropic principle is the argument that life-free universes cannot be observed, and observations of these counter-examples would be required in order to falsify the strong anthropic principle. However, this extension of anthropic ideas does have some attractions. Much weak anthropic reasoning invokes the generation of an ensemble of universes, but we have no idea whether such a concept is valid. It does apply to certain forms of inflationary cosmology, but it is equally possible that there is only one universe. In this case of a unique event, the arguments of statistical selection effects that lie at the core of weak anthropic reasoning are less satisfying; was it inevitable that life should arise on the one occasion that it has a chance? A possible position here is that the universe was designed for life, but this does not constitute a mechanism within the bounds of physics for enforcing a strong anthropic principle. It is consistent with the facts, but is in no way a proof for the existence of a creator. More profitable ideas are to be found in the area of the interpretation of quantum mechanics, which is a topic discussed to some extent in chapter 6 (chapter 7 of Barrow & Tipler 1986 gives a full discussion of the relation between quantum and anthropic ideas). Here, the role of the observer is critical in determining how the universe evolves. In the (almost) standard ``Copenhagen'' interpretation, the critical events in time are the moments of wave-function collapse when the act of observation singles out a concrete state from undetermined possibilities (e.g. spin up or down?). In this sense, the act of the observer is necessary in order to bring the universe into being at all.

PROBLEMS

(3.1) Show that the Robertson-Walker metric satisfies Einstein's equations and obtain the Friedmann equation(s).

(3.2) An object is observed at redshift z in a Friedmann universe with density parameter . Calculate the observed rate of change of redshift for the object. What fractional precision in observed frequency would be needed to detect cosmological deceleration in a decade?

(3.3) An object at comoving radius r is observed at two periods six months apart, allowing the parallax angle 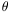to be observed for a baseline of D perpendicular to the line of sight. Show that the parallax distance D / 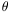is R₀ S_k (r) / C_k (r) and give an expression for this valid to second order in redshift.

(3.4) Consider the second-order corrections to the relation between redshift and angular-diameter distance [c / H₀] D(z):

(3.109)

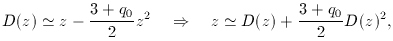
to second order. Attempt to account for this relation with a Newtonian analysis.

(3.6) The steady-state universe has R 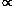e^Ht, zero curvature of its comoving coordinates (k = 0), and a proper density of all objects that is constant in time. Show that the comoving volume out to redshift z is V (z) = 4 (cz / H)³ / 3, and hence that the number-count slope for objects at typical redshift z becomes 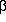= [(3 + ) ln z]^-1 for z >> 1, where is the spectral index of the objects.