3. WHAT THE CMB DATA ALONE TELL US

As a good first approximation, one should think of a map of the CMB anisotropy as a picture of the universe at a redshift of z_dec = 1089, when the CMB decoupled from the primordial plasma. Thus, the CMB tells us about the universe when it was less than t_dec = 379 kyrs old and a much simpler place. In this epoch, the early universe acts as though it is spatially flat, independent of the values of the dark energy and dark matter today.

The variation in temperature from spot to spot across the sky arises from the primordial plasma responding to spatial variations in the gravitational potential. In turn, the gravitational landscape is the manifestation of quantum fluctuations in some primordial field. In the inflationary model, one imagines these fluctuations stretched by at least 10²⁸ so that they are super-horizon size, and then expanded with the expansion of the universe.

Observing the CMB is like looking at a distant surface ⁽²⁾ at the edge of the observable universe. As the universe expands, the pattern in the anisotropy will shift as new regions of the gravitational landscape are sampled. For example, one may imagine that the quadrupole (l = 2) may rotate 90° in one Hubble time (30 mas/century), with higher multipoles changing faster. In a similar vein, the light from the clusters of galaxies that formed in the potential wells that gave rise to cold regions on the decoupling surface has not has enough time to reach us.

The processes of the formation of stars, galaxies, and clusters of galaxies takes place between us and the decoupling surface. As a first approximation, photons from the decoupling surface come to us unimpeded. The lower redshift properties do, though, affect the light from the decoupling surface but in characteristic and definable ways as discussed below.

A full analysis of the CMB involves accurately comparing the measured power spectrum, Figure 2, to models. The simplest model that describes the CMB data is flat and lambda-dominated. The results for this parametrization derived from WMAP alone (Spergel et al. 2003) and the independent GUS analysis are shown in Table 1.

Table 1. Cosmic Parameters from CMB measurements

Description	Parameter	WMAP	GUS	w/2dF
Baryon density	b h2	0.024 ± 0.001	0.023 ± 0.002	0.023 ± 0.001
Matter density	m h2	0.14 ± 0.02	0.14 ± 0.01	0.134 ± 0.006
Hubble parameter	h	0.72 ± 0.05	0.71 ± 0.05	0.73 ± 0.03
Amplitude	A	0.9 ± 0.1	0.85 ± 0.06	0.8 ± 0.1
Spectral index	ns	0.99 ± 0.04	0.967 ± 0.029	0.97 ± 0.03
Optical depth		0.166+0.076-0.071	...	0.148 ± 0.072

We can get at the essence of what the CMB is telling us from the following. Let us focus on the decoupling surface. There is a natural length scale in the early universe that is smaller than the horizon size. It corresponds to the distance over which a density perturbation (sound wave) in the primordial plasma can propagate in the age of the universe at the time of decoupling (t_dec = 379 kyr). It is called the acoustic horizon. Once we know the contents of the universe from the overall characteristics of the power spectrum, we can compute the size of the acoustic horizon. It is roughly r_s 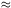c_s t_dec z_dec where c_s is the sound speed in the plasma. In the full expression (Hu & Sugiyama 1995), r_s depends on only the physical densities of matter and radiation and not on the Hubble parameter, h. We may think of r_s as a standard yard stick embedded in the decoupling surface. From a map of the anisotropy, we measure the angular size, 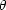_A, of the feature corresponding to r_s. From WMAP, 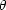_A = 0.598° ± 0.002. By definition then,

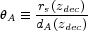(1)

where d_A is the angular size distance to the decoupling surface. In d_A we can trade off the geometry, _k = 1 - _r - _m - 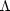, with h. Thus to determine the geometry without recourse to appealing to the simplest model, we must make a prior assumption on h. The dependence is not strong. If one assumes h > 0.5 then one finds 0.98 < _tot < 1.08 (95% cl), where again we have used the WMAP data for illustration. The progress in our knowledge of _tot as determined by all available data roughly between the past two IAU symposia (starting with Figure 1, Bond et al. 2003) is:

Table 2. Total Cosmic Density, _tot (1 errors)

January 2000	tot = 1.06+0.16-0.10
January 2002	tot = 1.035+0.043-0.046
January 2003	tot = 1.034+0.040-0.042
March 2003 (+WMAP)	tot = 1.015+0.063-0.015

One way to see what the CMB alone can tell us is to plot the data in the _m - 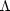plane for a pure cosmological constant, or equation of state w = -1. This is shown in Figure 4 for the WMAP data. All simple open, flat, and closed cosmological models satisfying the Friedmann equation can be plotted here. One picks a point in the space, a single source of the fluctuations (e.g., adiabatic fluctuations in the metric from an inflationary epoch), w = -1, and marginalizes over the other parameters (n_s, _b, , A) with uniform priors. The possibilities are labeled by the Hubble parameter that goes with them.

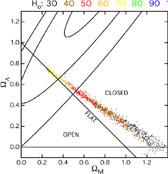Figure 4. Models consistent with the WMAP CMB data in the - m plane. The flat models correspond to the line with + m = 1. This plot assumes that the dark energy has w = -1. The code at the top gives the values of the Hubble constant as one moves along the geometric degeneracy. It is striking that the value picked out by the CMB for a flat universe, h = 0.71, is in such agreement with the value from the HST key project. The observations behind these two probes are completely different and correspond to times separated by a good fraction the age of the universe. The 1, 2, and 3 contours for the supernovae are plotted as well (Tonry et al. 2003). Constraints from large scale structure would correspond to roughly a vertical swath centered on m = 0.3. This plot is courtesy of Ned Wright.

There are a number of things the plot pulls together. First, there is a large degeneracy in the CMB data along the line that runs above the line for flat universe. This is called the "geometric degeneracy" and is essentially the observation noted above that one must pick h to determine d_A to complete the equation 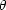_A = r_s / d_A. The degeneracy line clearly misses a model in which the universe is flat with _m = 1 ( 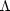= 0), the Einstein-deSitter case. 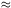If one stretches the data slightly, it is possible to have a model with _m 1.3 ( 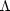= 0) but the price one pays is a Hubble parameter near 0.3. This value is in conflict with a host of other non-CMB observations. In addition, when one considers the Integrated Sachs-Wolfe (ISW) induced cross-correlation between cosmic structure, as measured by radio sources, and the CMB anisotropy, this solution is disfavored at the 3 level (Nolta et al. 2003). Thus, in this minimal picture, there are no models with 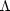= 0 that fit the data.

Once one moves off the x axis, the intersection of the flat universe line, 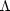+ _m = 1, and the geometric degeneracy is the next least baroque point, at least by today's standards of baroqueness. It is very satisfying that h for the intersection is very close to the value obtained from the Hubble Key Project (h = 0.72 ± 0.03(stat) ± 0.07(sys), Freedman et al. 2001). Additionally, the values agree with probes of the large scale structure and the supernovae data. From the plot, it is easy to see why such a weak prior on h (or _m) picks out a flat universe. A number have noted that all determinations of _tot are greater than unity. The plot shows that with the priors we have chosen, there are more solutions with _tot > 1. This may bias the solution somewhat.

² This is the "surface" at which the CMB decoupled from the primordial electrons and baryons. It is sometimes called the last scattering surface, but since 15% of the CMB photons were really last scattered when the universe was reionized near z = 20, we prefer decoupling. Back.