


2.5. The nearest neighbour method
The nearest neighbour class of estimators represents an attempt to
adapt the amount of smoothing to the `local' density of data. The
degree of smoothing is controlled by an integer k, chosen to be
considerably smaller than the sample size; typically
k 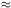 n1/2. Define
the distance d (x, y) between two points on the
line to be |x - y| in the
usual way, and for each t define
n1/2. Define
the distance d (x, y) between two points on the
line to be |x - y| in the
usual way, and for each t define
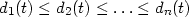
|
to be the distances, arranged in ascending order, from t to the points of the sample.
The kth nearest neighbour density estimate is then defined by
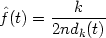
| (2.3) |
In order to understand this definition, suppose that the density at t is f (t). Then, of a sample of size n, one would expect about 2r n f (t) observations to fall in the interval [t - r, t + r] for each r > 0; see the discussion of the naive estimator in Section 2.3 above. Since, by definition, exactly k observations fall in the interval [t - dk(t), t + dk(t)], an estimate of the density at t may be obtained by putting
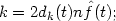
|
this can be rearranged to give the definition of the kth nearest neighbour estimate.
While the naive estimator is based on the number of observations falling in a box of fixed width centred at the point of interest, the nearest neighbour estimate is inversely proportional to the size of the box needed to contain a given number of observations. In the tails of the distribution, the distance dk(t) will be larger than in the main part of the distribution, and so the problem of undersmoothing in the tails should be reduced.
Like the naive estimator, to which it is related, the nearest choice
neighbour estimate as defined in (2.3) is not a smooth curve. The
function dk(t) can easily be seen to be
continuous, but its derivative
will have a discontinuity at every point of the form
1/2(X(j) + X(j+k)),
where X(j) are the order statistics of the sample. It
follows at once from
these remarks and from the definition that
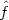 will be
positive and
continuous everywhere, but will have discontinuous derivative at all
the same points as dk. In contrast to the kernel
estimate, the nearest
neighbour estimate will not itself be a probability density, since it
will not integrate to unity. For t less than the smallest data
point, we will have
dk(t) = X(n-k+1) and for
t > X(n) we will have
dk(t) = t -
X(n-k+1). Substituting into (2.3), it follows that
will be
positive and
continuous everywhere, but will have discontinuous derivative at all
the same points as dk. In contrast to the kernel
estimate, the nearest
neighbour estimate will not itself be a probability density, since it
will not integrate to unity. For t less than the smallest data
point, we will have
dk(t) = X(n-k+1) and for
t > X(n) we will have
dk(t) = t -
X(n-k+1). Substituting into (2.3), it follows that
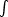 -
-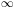
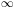
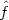 die away
at rate t-1, in other words
extremely slowly. Thus the nearest neighbour estimate is unlikely to
be appropriate if an estimate of the entire density is required.
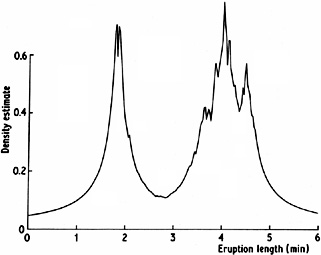
Figure 2.10 gives a nearest neighbour density
estimate for the Old
Faithful data. The heavy tails and the discontinuities in the derivative
are clear.
die away
at rate t-1, in other words
extremely slowly. Thus the nearest neighbour estimate is unlikely to
be appropriate if an estimate of the entire density is required.
Figure 2.10 gives a nearest neighbour density
estimate for the Old
Faithful data. The heavy tails and the discontinuities in the derivative
are clear.
|
Fig. 2.10 Nearest neighbour estimate for Old Faithful geyser data, k = 20. |
It is possible to generalize the nearest neighbour estimate to provide an estimate related to the kernel estimate. As in Section 2.4, let K(x) be a kernel function integrating to one. Then the generalized kth nearest neighbour estimate is defined by
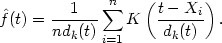
| (2.4) |
It can be seen at once that
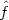 (t) is precisely the kernel estimate
evaluated at t with window width dk(t). Thus
the overall amount of
smoothing is governed by the choice of the integer k, but the window
width used at any particular point depends on the density of
observations near that point.
(t) is precisely the kernel estimate
evaluated at t with window width dk(t). Thus
the overall amount of
smoothing is governed by the choice of the integer k, but the window
width used at any particular point depends on the density of
observations near that point.
The ordinary kth nearest neighbour estimate is the special case of (2.4) when K is the uniform kernel w of (2.1); thus (2.4) stands in the to same relation to (2.3) as the kernel estimator does to the naive ed. estimator. However, the derivative of the generalized nearest neighbour estimate will be discontinuous at all the points where the function dk(t) has discontinuous derivative. The precise integrability and tail properties will depend on the exact form of the kernel, and to will not be discussed further here.
Further discussion of the nearest neighbour approach will be given in Section 5.2.