A. The theories

1. General relativity

Some early discussions of the cosmological tests, as in Robertson (1955) and Bondi (1960), make the point that observationally important elements of a spatially homogeneous cosmology follow by symmetry, independent of general relativity. This means some empirical successes of the cosmology are not tests of relativity. The point was important in the 1950s, because the Steady State theory was a viable alternative to the Friedmann-Lemaître cosmology, and because the experimental tests of relativity were quite limited.

The tests of general relativity are much better now, but cosmology still is a considerable extrapolation. The length scales characteristic of the precision tests of general relativity in the Solar System and binary pulsar are 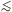10¹³ cm. An important scale for cosmology is the Hubble length, H₀^-1 ~ 5000 Mpc ~ 10²⁸ cm, fifteen orders of magnitude larger. An extrapolation of fifteen orders of magnitude in energy from that achieved at the largest accelerators, ~ 10¹² eV, brings us to the very different world of the Planck energy. Why is the community not concerned about an extrapolation of similar size in the opposite direction? One reason is that the known open issues of physics have to do with small length scales; there is no credible reason to think general relativity may fail on large scales. This is comforting, to be sure, but, as indicated in footnote 7, not the same as a demonstration that we really know the physics of cosmology. Another reason is that if the physics of cosmology were very different from general relativity it surely would have already been manifest in serious problems with the cosmological tests. This also is encouraging, but we have to consider details, as follows.

One sobering detail is that in the standard cosmology the two dominant contributions to the stress-energy tensor - dark energy and dark matter - are hypothetical, introduced to make the theories fit the observations (Eq. [2]). This need not mean there is anything wrong with general relativity - we have no reason to expect Nature to have made all matter readily observable other than by its gravity - but it is a cautionary example of the challenges. Milgrom's (1983) modified Newtonian dynamics (MOND) replaces the dark matter hypothesis with a hypothetical modification of the gravitational force law. MOND gives remarkably successful fits to observed motions within galaxies, without dark matter (de Blok et al., 2001). So why should we believe there really is cosmologically significant mass in nonbaryonic dark matter? Unless we are lucky enough to get a laboratory detection, the demonstration must be through the tests of the relativistic cosmology (and any other viable cosmological models that may come along, perhaps including an extension of MOND). This indirect chain of evidence for dark matter is becoming tight. A new example - the prospect for a test of the inverse square law for gravity on the length scales of cosmology - is striking enough for special mention here.

Consider the equation of motion ⁽⁵⁸⁾ of a freely moving test particle with nonrelativistic peculiar velocity 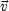in a universe with expansion factor a(t),

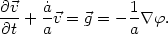(51)

The particle always is moving toward receding observers, which produces the second term in the left-most expression. The peculiar gravitational acceleration 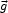relative to the homogeneous background model is computed from the Poisson equation for the gravitational potential ,

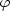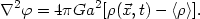(52)

The mean mass density <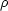> is subtracted because 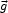is computed relative to the homogeneous model. The equation of mass conservation expressed in terms of the density contrast 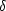= 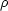/ <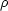> - 1 of the mass distribution modeled as a continuous pressureless fluid is

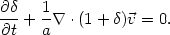(53)

In linear perturbation theory in 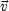and 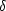these equations give

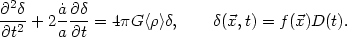(54)

Here D(t) is the growing solution to the first equation. ⁽⁵⁹⁾ The velocity field belonging to the solution D(t) is the inhomogeneous solution to Eq. (53) in linear perturbation theory,

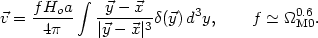(55)

The factor f = d log D / d log a depends on the cosmological model; the second equation is a good approximation if 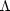= 0 or space curvature vanishes. ⁽⁶⁰⁾ One sees from Eq. (55) that the peculiar velocity is proportional to the gravitational acceleration, as one would expect in linear theory.

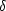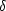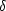
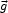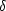
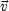
The key point of Eq. (54) for the present purpose is that the evolution of the density contrast at a given position is not affected by the value of anywhere else. This is a consequence of the inverse square law. The mass fluctuation in a chosen volume element produces a peculiar gravitational acceleration that produces a peculiar velocity field 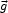that has zero divergence and so has no effect on the mass distribution outside the volume element.

For a "toy" model of the effect of a failure of the inverse square law, suppose we adjust the expression for the peculiar gravitational acceleration produced by a given mass distribution to

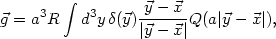(56)

where R is some function of world time only. In standard gravity physics Q(w) = w^-2. We have no basis in fundamental physics for any other function of w. Although Milgrom's (1983) MOND provides a motivation, Eq. (56) is not meant to be an extension of MOND to large-scale flows. It is an ad hoc model that illustrates an important property of the inverse square law.

We noted that in linear theory 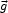. Thus we find that the divergence of Eq. (56), with the mass conservation equation (53) in linear perturbation theory, gives

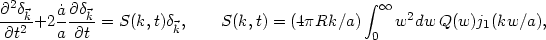(57)

where 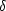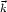(t) is the Fourier transform of the mass density contrast 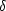(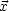, t) and j₁ is a spherical Bessel function. The inverse square law, Q = w^-2, makes the factor S independent of the wavenumber k. This means all Fourier amplitudes grow by the same factor in linear perturbation theory (when the growing mode dominates), so the functional form of 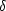(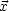, t) is preserved and the amplitude grows, as Eq. (54) says. 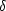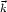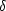When Q is some other function, the phases of the are preserved but the functional form of the power spectrum |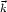|² evolves. For example, if Q 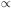w^{n - 2} with -2 < n < 1 (so the integral in Eq. [57] does not diverge) Eq. (57) is

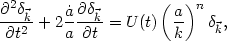(58)

where U is some function of world time.

If n > 0 density fluctuations grow faster on larger scales. If Q(w) follows Newtonian gravity on the scale of galaxies and bends to n > 0 on larger scales it reduces the mean mass density needed to account for the measured large-scale galaxy flows, and maybe reduces the need for dark matter. But there are testable consequences: the apparent value of _M0 would vary with the length scale of the measurement, and the form of the power spectrum of the present mass distribution would not agree with the form at redshift z ~ 1000 when it produced the observed angular power spectrum of the 3 K cosmic microwave background. Thus we are very interested in the evidence of consistency of these tests (as discussed in Sec. IV.B.13).

⁵⁸ These relations are discussed in many books on cosmology, including Peebles (1980a). Back.

⁵⁹ The general solution is a sum of the growing and decaying solutions, but because the universe has expanded by a large factor since nongravitational forces were last important on large scales we can ignore the decaying part. Back.

⁶⁰ This is illustrated in Fig. 13.14 in Peebles (1993). An analytic expression for spherical symmetry is derived by Lightman and Schechter (1990). Back.