


In this section we will provide just a quick description of the
remarkable cosmological features of cosmic strings.
Many of the proposed observational tests for the existence of cosmic
strings are based on their gravitational interactions. In fact, the
gravitational field around a straight static string is very unusual
[Vilenkin, 1981].
As is well known, the Newtonian limit of Einstein field equations with
source term given by Tµ =
diag(
=
diag( ,
-p1, -p2, -p3)
in terms of the Newtonian potential
,
-p1, -p2, -p3)
in terms of the Newtonian potential
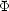 is given by
is given by
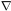 2
2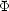 =
4
=
4 G
(
G
( +
p1 + p2 + p3),
just a statement of
the well known fact that pressure terms also contribute to the
`gravitational mass'. For an infinite string in the z-direction one
has p3 =
-
+
p1 + p2 + p3),
just a statement of
the well known fact that pressure terms also contribute to the
`gravitational mass'. For an infinite string in the z-direction one
has p3 =
- , i.e.,
strings possess a large relativistic
tension (negative pressure). Moreover, averaging on the string core
results in vanishing
pressures for the x and y directions yielding
, i.e.,
strings possess a large relativistic
tension (negative pressure). Moreover, averaging on the string core
results in vanishing
pressures for the x and y directions yielding
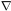 2
2
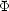 = 0
for the Poisson equation. This indicates that space is flat outside of
an infinite straight cosmic string and therefore test particles in its
vicinity should not feel any gravitational attraction.
= 0
for the Poisson equation. This indicates that space is flat outside of
an infinite straight cosmic string and therefore test particles in its
vicinity should not feel any gravitational attraction.
In fact, a full general relativistic analysis confirms this and test
particles in the space around the string feel no Newtonian attraction;
however there exists something unusual, a sort of wedge missing from
the space surrounding the string and called the `deficit angle',
usually noted 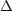 , that
makes the topology of space around the string that of a cone.
To see this, consider the metric of a source with energy-momentum
tensor [Vilenkin 1981,
Gott 1985]
, that
makes the topology of space around the string that of a cone.
To see this, consider the metric of a source with energy-momentum
tensor [Vilenkin 1981,
Gott 1985]
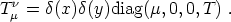
| (75) |
In the case with T = µ (a rather simple equation of state) this is the effective energy-momentum tensor of an unperturbed string with string tension µ as seen from distances much larger than the thickness of the string (a Goto-Nambu string). However, real strings develop small-scale structure and are therefore not well described by the Goto-Nambu action. When perturbations are taken into account T and µ are no longer equal and can only be interpreted as effective quantities for an observer who cannot resolve the perturbations along its length. And in this case we are left without an effective equation of state. Carter [1990] has proposed that these `noisy' strings should be such that both its speeds of propagation of perturbations coincide. Namely, the transverse (wiggle) speed cT = (T / µ)1/2 for extrinsic perturbations should be equal to the longitudinal (woggle) speed cL = (-dT / dµ)1/2 for sound-type perturbations. This requirement yields the new equation of state
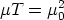
| (76) |
and, when this is satisfied, it describes the energy-momentum tensor of a wiggly string as seen by an observer who cannot resolve the wiggles or other irregularities along the string [Carter 1990, Vilenkin 1990].
The gravitational field around the cosmic string [neglecting terms of
order (Gµ)2] is found by solving the
linearized Einstein
equations with the above Tµ . One gets
. One gets
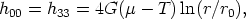
| (77) |
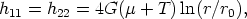
| (78) |
where hµ = gµ
= gµ -
- 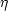 µ
µ is the metric perturbation, the radial distance from the string is
r = (x2 + y2)1/2,
and r0 is a constant of integration.
is the metric perturbation, the radial distance from the string is
r = (x2 + y2)1/2,
and r0 is a constant of integration.
For an ideal, straight, unperturbed string, the tension and mass per unit length are T = µ = µ0 and one gets
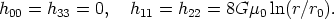
| (79) |
By a coordinate transformation one can bring this metric to a locally flat form
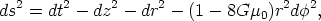
| (80) |
which describes a conical and flat (Euclidean) space with a wedge of
angular size 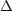 =
8
=
8 G
µ0 (the deficit angle) removed from
the plane and with the two faces of the wedge identified.
G
µ0 (the deficit angle) removed from
the plane and with the two faces of the wedge identified.
Wakes and gravitational lensing
We saw above that test particles
(15) at rest in the
spacetime of the straight string experience no gravitational force,
but if the string moves the situation radically changes. Two particles
initially at rest while the string is far away, will suddenly begin
moving towards each other after the string has passed between
them. Their head-on velocities will be proportional to
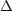 or,
more precisely, the particles will get a boost v =
4
or,
more precisely, the particles will get a boost v =
4 Gµ0 vs
Gµ0 vs
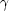 in the
direction of the surface swept out by the string.
Here,
in the
direction of the surface swept out by the string.
Here, 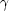 =
(1-vs2)-1/2 is the
Lorentz factor and vs the
velocity of the moving string. Hence, the moving string will built up
a wake of particles behind it that may eventually form the
`seed' for accreting more matter into sheet-like structures
[Silk & Vilenkin
1984].
=
(1-vs2)-1/2 is the
Lorentz factor and vs the
velocity of the moving string. Hence, the moving string will built up
a wake of particles behind it that may eventually form the
`seed' for accreting more matter into sheet-like structures
[Silk & Vilenkin
1984].
Also, the peculiar topology around the string makes it act as a
cylindric gravitational lens that may produce double images of distant
light sources, e.g., quasars. The angle between the two images
produced by a typical GUT string would be
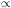 Gµ
and of order
of a few seconds of arc, independent of the impact parameter and with
no relative magnification between the images [see
Cowie & Hu, 1987,
for a recent observational attempt].
Gµ
and of order
of a few seconds of arc, independent of the impact parameter and with
no relative magnification between the images [see
Cowie & Hu, 1987,
for a recent observational attempt].
The situation gets even more interesting when we allow the string to have small-scale structure, which we called wiggles above, as in fact simulations indicate. Wiggles not only modify the string's effective mass per unit length, µ, but also built up a Newtonian attractive term in the velocity boost inflicted on nearby test particles. To see this, let us consider the formation of a wake behind a moving wiggly string. Assuming the string moves along the x-axis, we can describe the situation in the rest frame of the string. In this frame, it is the particles that move, and these flow past the string with a velocity vs in the opposite direction. Using conformally Minkowskian coordinates we can express the relevant components of the metric as
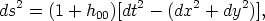
| (81) |
where the missing wedge is reproduced by identifying the half-lines
y = ±4  G
µx, x
G
µx, x
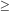 0.
The linearized geodesic equations in this metric can be written as
0.
The linearized geodesic equations in this metric can be written as
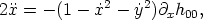
| (82) |
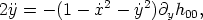
| (83) |
where over-dots denote derivatives with respect to t. Working to first order in Gµ, the second of these equations can be integrated over the unperturbed trajectory x = vs t, y = y0. Transforming back to the frame in which the string has a velocity vs yields the result for the velocity impulse in the y-direction after the string has passed [Vachaspati & Vilenkin, 1991; Vollick, 1992]
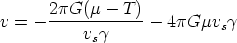
| (84) |
The second term is the velocity impulse due to the conical deficit
angle we saw above. This term will dominate for large string
velocities, case in which big planar wakes are predicted. In this
case, the string wiggles will produce inhomogeneities in the wake and
may easy the fragmentation of the structure. The `top-down' scenario
of structure formation thus follows naturally in a universe with
fast-moving strings. On the contrary, for small velocities, it is the
first term that dominates over the deflection of particles. The origin
of this term can be easily understood
[Vilenkin & Shellard,
2000].
From Eqn. (77), the gravitational force on a
non-relativistic particle of mass m is F ~ m
G(µ- T) /r. A
particle with an impact parameter r is exposed to this force for a
time 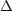 t
~ r / vs and the resulting velocity is v
~ (F / m)
t
~ r / vs and the resulting velocity is v
~ (F / m)
 t
~ G(µ- T) / vs.
t
~ G(µ- T) / vs.
15 If one takes into account the own gravitational field of the particle living in the spacetime around a cosmic string, then the situation changes. In fact, the presence of the conical `singularity' introduced by the string distorts the particle's own gravitational field and results in the existence of a weak attractive force proportional to G2µm2 / r2, where m is the particle's mass [Linet, 1986]. Back.