Annu. Rev. Astron. Astrophys. 1984. 22: 471-506 Copyright © 1984 by Annual Reviews. All rights reserved

4. BLACK HOLES ACCORDING TO GENERAL RELATIVITY

The physics of dense star clusters and of supermassive objects are complex and poorly understood. In contrast, the final state of such systems - if gravitational collapse indeed occurs - is comparatively simple, at least if we accept general relativity. According to the so-called no-hair theorems, the endpoint of a gravitational collapse, however messy and asymmetrical it may have been, is a standardized black hole characterized by just two parameters - mass and spin - and described exactly by the Kerr metric. If the collapse occurred in a violent or sudden way, it would take several dynamical time scales for the hole to settle down; during that period, gravitational waves would be emitted. But the final state would still be the Kerr solution, unless the material left behind constituted a strong perturbation. [The perturbation due to the infalling material in steady accretion flows is a negligible perturbation by a wide margin of order (r_g / c) / t_E.]

The expected spin of the hole - an important influence on its observable manifestations - depends on the route by which it formed (see Figure 1). A precursor spinning fast enough to be significantly flattened by rotational effects when its radius was >> r_g would probably have more specific angular momentum than the critical value GM/c. A massive black hole that forms "in one go" is thus likely to have been fed with as much spin as it can accept and to end up near the top of the range of angular momentum permitted by the Kerr metric; the same is true for holes that grow by gradual accretion of infalling galactic gas (11) (though the expectation is less clear if they grow by tidal disruption of stars). We should therefore take full cognizance of the distinctive properties of spinning black holes.

4.1. The Kerr Metric

The Kerr metric changes its character, and the event horizon disappears, if the specific angular momentum J = J_max = GM / c. The so-called cosmic censorship hypothesis would then require that holes always form with J < J_max. The Kerr solution then has a critical radius called the static limit, within which particles must corotate with the hole, though they can still escape. This arises because the frame-dragging is so strong that even light cones necessarily point in the direction. This critical surface, with equatorial radius

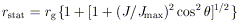
(17)

is not the event horizon itself; the latter occurs at a smaller radius. The region between the event horizon (r = r_EH) and the static limit is called the "ergosphere," because one can in principle extract energy from it via a process first proposed by Penrose (96): a particle entering the ergosphere can split in two in such a way that one fragment falls into the hole, but the other leaves the ergosphere with more energy than the original particle. The extra energy comes from the hole itself. A Kerr hole can be considered to have two kinds of mass-energy: a fraction associated with its spin, which can be extracted via the Penrose process, and an "irreducible" mass (14, 41). The fraction that can in principle be extracted is

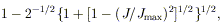
(18)

which is 29% for a maximally rotating hole. The above limit is an instance of a general theorem in black hole physics, according to which the area of the event horizon (a quantity analogous to entropy) can never decrease: a Kerr hole has smaller surface area than a Schwarzschild hole of the same mass. There have been various attempts to incorporate Penrose-style energy extraction into a realistic astrophysical model (64, 100). Those mechanisms that involve particle collisions or scattering operate only for a special subset of trajectories (14), and they would be swamped by accompanying processes. However, a process involving electromagnetic effects - the Blandford-Znajek mechanism (29) - seems more promising (and is discussed further below and in Section 5).

ORBITS     The binding energy per unit mass for a circular orbit of radius around a Schwarzschild hole (with J = 0) is

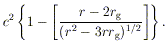
(19)

For r >> r_g this reduces to G M/2r, which is just the Newtonian binding energy. However, the binding energy has a maximum of 0.057c for an orbit at r_min = 6r_g, with angular momentum _min = 2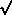3 r_g c. Circular orbits closer in than this have more angular momentum and are less tightly bound (as for orbits in classical theory when the effective force law is 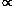r^-n, with n > 3): the orbits have zero binding energy for r = 4r_g (with corresponding angular momentum 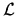₀ = 4r_g c); and for r = 3r_g, the expression (19.) goes to infinity, which implies that photons can move in circular orbits at this radius. In the Kerr metric, the behavior of orbits depends on their orientation with respect to the hole and on whether they are corotating or counterrotating (14). For corotating equatorial orbits, the innermost stable orbit moves inward (as compared with the Schwarzschild case); it becomes more tightly bound, with a smaller 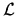_min. For (J/J_max) > 0.94, r_min actually lies within the ergosphere. As J -> J_max the stable corotating orbits extend inward toward r = r_g, and their binding energy approaches (1 - 3^-1/2)c = 0.42c. These numbers determine the maximum theoretical efficiency of accretion disks.

4.2. Three Astrophysically Important Relativistic Effects

THE MINIMUM ANGULAR MOMENTUM     An important inference from the above is that there are no stationary bound orbits whose angular momentum is less than a definite threshold value: particles whose angular momentum is too low plunge directly into the hole. This qualitative feature of the orbits means that no stationary axisymmetric flow pattern can extend too close to the rotation axis of a black hole (even well away from the equatorial plane) - no such constraint arises for flows around an object with a "hard" surface. Many authors have suggested that the resultant "funnels" play a role in the initial bifurcation and collimation of jets.

LENSE-THIRRING PRECESSION     An orbit around a spinning (Kerr) hole that does not lie in the equatorial plane precesses around the hole's spin axis with an angular velocity [discussed by Bardeen & Petterson (13)] of

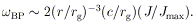
(20)

This precession has a time scale longer than the orbital period by a factor of ~ (r / r_g)^3/2(J / J_max)^-1. However, if material spirals slowly inward (at a rate controlled by viscosity) in a time much exceeding the orbital time, then the effects of this precession can mount up. The important consequence follows that the flow pattern near a black hole, within the radius where 2 / _BP, is less than the inflow time, can be axisymmetric with respect to the hole irrespective of the infalling material's original angular momentum vector. The Lense-Thirring precession, an inherently relativistic effect, thus guarantees that a wide class of flow patterns near black holes will be axisymmetric - an important simplification of the problem.

ELECTROMAGNETIC PROPERTIES OF BLACK HOLES     Interactions of black holes with magnetic fields imposed on their surroundings can have important astrophysical effects. When a hole forms from collapsing magnetized material, the magnetic field outside the horizon decays ("redshifts away") on the collapse time scale r_g / c. But if, for instance, an external electric field were applied to a Schwarzschild hole, then after transients had decayed, a modified field distribution would be established where the electric field appeared to cross the horizon normally. The event horizon (or "surface") of the hole thus behaves in some respects like a conductor (47, 76, 134). It does not have perfect conductivity, however: if it did, electromagnetic flux would never be able to penetrate the horizon. Comparing the decay time scale for transients around a black hole (r_g / c) with the time scale (r_g² / 4 ) appropriate to a sphere of radius r_g and conductivity , we can associate a surface resistivity of 377 with the horizon. This analogy can be put on a more rigorous basis (134), and the "resistance" of a black hole is found to be Z_H 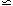100 ohms. More generally, a Kerr black hole behaves like a spinning conductor. A simple discussion (98) valid for J << J_max shows that a hole embedded in a uniform magnetic field B₀ would acquire a quadrupole distribution of electric charge

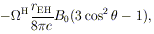
(21)

where _H = (J / J_max) c / 2r_EH is the effective angular velocity of the hole. The corresponding poloidal electric field in a nonrotating frame is

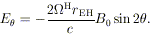
(22)

Just as in a classical "unipolar inductor," power can be extracted by allowing a current flow between a spinning hole's equator and poles. The maximum electric potential drop is ~ B₀ r_g(J / J_max), where B₀ is the imposed field. This can be very large, as it is when a similar argument is applied to spinning magnetized neutron stars in conventional models for pulsars.

For the fiducial field strength B_E (Equation 6), this emf is

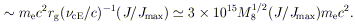
(23)

A single test charge introduced into this electromagnetic field will extract from the hole an energy of this order. However, the magnetosphere is unlikely just to contain a few "test charges"; indeed, the bare minimum charge density needed to modify the imposed field is

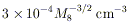
(24)

(cf. Equation 12), and pair production generates far more charges than this (see Section 5). Just as in pulsars (8), a realistic magnetospheric current system and plasma distribution, though very hard to calculate, is likely to "short-out" the electric field. A relevant parameter is then _H, the angular velocity of the field lines at large distance from the hole. This is related to the ratio of the effective resistance Z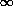 to the resistance of the hole Z_H:

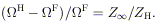
(25)

In the charge-starved limit, corresponding to infinite resistance at infinity, ^F = 0. The "matched" case when Z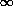 = Z_F(^F = ½ ^H) corresponds to the maximum power extraction for a given B₀. This power is of order

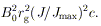
(26)

The efficiency in this case is lower than when Z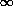 -> 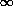(zero power), in the sense that half of the power is dissipated in the hole, and raises its irreducible mass; nevertheless, 9.2% of the rest energy could be extracted while slowing down a hole that started off with J = J_max.

Electromagnetic extraction of energy from black holes seems a realistic and important possibility. Its astrophysical context is discussed in Section 5.

SUMMARY     The results of this section can be summarized by saying that three distinctively relativistic features of black holes are important in models for galactic nuclei:

1. There is a definite lower limit to the angular momentum of any stably orbiting material.

2. The Lense-Thirring precession enforces axisymmetry on any inward-spiraling flow pattern near the hole; consequently, any directed outflow initiated in the relativistic domain will be aligned with the hole's spin axis and will squirt in a constant direction (irrespective of the provenance of the infalling gas), except insofar as precession or accretion processes can reorient the hole's spin (105).

3. A rotating hole's latent spin energy can be tapped by externally applied magnetic fields; this can provide a power source far exceeding that from the accretion process itself.