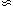 0.7). This component
could be produced by non-zero and positive cosmological constant
Λ with
0.7). This component
could be produced by non-zero and positive cosmological constant
Λ with
Adapted from a contributed talk at the 2nd Hellenic Cosmology Workshop at NOA (Athens) Jan. 2001
Recent cosmological observations extending the
Hubble diagram of high redshift Type Ia supernovae performed
independetly by two groups (the Supernova Cosmology Project
[2]
and the High-Z Supernova Team
[3,
4]
presented evidence that the expansion of the Universe is accelerating
rather than slowing down. This fact combined with the Boomerang and
Maxima-1 measurements of the first acoustic peak location in the
angular power spectrum of the cosmic microwave background (CMB)
[5,
6]
point towards a standard cosmological model with critical density
(Ω =
Ωm +
ΩΛ = 1) and a
dominant Λ-like, "dark
energy" component at the present epoch
(ΩΛ
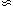 0.7). This component
could be produced by non-zero and positive cosmological constant
Λ with
0.7). This component
could be produced by non-zero and positive cosmological constant
Λ with
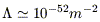
| (1) |
Such a term can produce the required repulsive force to explain the accelerating universe phenomenon. A diverse set of other cosmological observations also compellingly suggest that the universe posesses a nonzero negative pressure component corresponding to vacuum energy density of the same order as the matter energy density [7, 8, 9]
In addition to causing an acceleration to the expansion of the universe the existence of a non-zero cosmological constant would have interesting gravitational effects on various astrophysical scales [10, 1]. For example it would affect gravitational lensing statistics of extragalactic surveys [11], large scale velocity flows [12] and there have been some claims that even smaller systems (galactic [13] and planetary [14]) could be affected in an observable way by the presence of a cosmological constant consistent with cosmological expectations. Even though some of these claims were falsified [15, 16, 17] the scale dependence of the dynamical effects of vacuum energy remains an interesting open issue.
The effects of the vacuum energy on cosmological scales and on local dynamics can be obtained from the Einstein equations which in the presence of a non-zero cosmological constant are written as
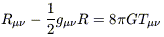
| (2) |
These equations, under the assumptions of spherical symmetric
energy-momentum (EM) tensor Tki =
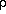 Q
c2;
diag(1, -w, -w, -w) and a mixture of
dust-like matter
(
Q
c2;
diag(1, -w, -w, -w) and a mixture of
dust-like matter
(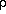 =
=
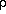 m,
w = 0) and dark energy
(
m,
w = 0) and dark energy
(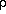 =
=
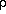 Q,
-1/3
Q,
-1/3 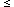 w
w
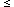 -1) lead (for the 1-1
component) to the generalized Newton's equation
-1) lead (for the 1-1
component) to the generalized Newton's equation
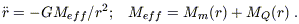
| (3) |
where M(r) = 4π/3
(1 + 3w)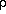 r3. Notice that for
w < -1/3 we have negative gravitating effective mass
(antigravity) which can lead to accelerated cosmological expansion
and to non-trivial dynamical effects on astrophysical scales. The
accelerated cosmological expansion is obtained for w < -1/3
from the Friedman equations which for k = 0 imply
r3. Notice that for
w < -1/3 we have negative gravitating effective mass
(antigravity) which can lead to accelerated cosmological expansion
and to non-trivial dynamical effects on astrophysical scales. The
accelerated cosmological expansion is obtained for w < -1/3
from the Friedman equations which for k = 0 imply
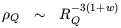
| (4) |
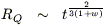
| (5) |
where RQ is the scale factor of the universe. In what
follows we focus on the effects of dark energy with w = -1
(cosmological cosntant). The more general case of -1 < w
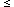 -1/3
([18])
will be discussed elsewhere.
-1/3
([18])
will be discussed elsewhere.
The vacuum energy implied from eq. (1) (10-10
erg/cm3) is less by many orders of magnitude than any sensible
estimate based on particle physics. In addition, the matter
density 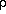 m and and the vacuum energy
m and and the vacuum energy
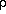 Λ evolve
at different rates, with
Λ evolve
at different rates, with
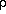 m /
m /
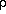 Λ
Λ
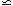 R-3 and
it would seem quite unlikely that they would differ today by a
factor of order unity. Interesting attempts have been made during
the past few years to justify this apparent fine tuning by
incorporating evolving scalar fields
([18]) or
probabilistic arguments based on the anthropic principle
[19]).
R-3 and
it would seem quite unlikely that they would differ today by a
factor of order unity. Interesting attempts have been made during
the past few years to justify this apparent fine tuning by
incorporating evolving scalar fields
([18]) or
probabilistic arguments based on the anthropic principle
[19]).
For w = -1 we have
Einstein's cosmological constant with
Λ = 8
π G
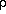 Λ / c2
(cosmological vacuum with w = -1) and the gravitating mass is
MΛ = -8
π
Λ / c2
(cosmological vacuum with w = -1) and the gravitating mass is
MΛ = -8
π
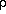 Λ r3 /
3. Thus the generalized Newtonian potential
leads to a gravitational interaction acceleration
Λ r3 /
3. Thus the generalized Newtonian potential
leads to a gravitational interaction acceleration
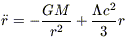
| (6) |
This generalized force includes a repulsive term
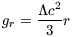
| (7) |
which is expected to dominate at distances larger than
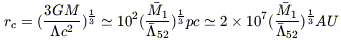
| (8) |
where 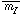 1 is the mass
within a sphere of radius rc in
units of solar masses
M
1 is the mass
within a sphere of radius rc in
units of solar masses
M = 2 ×
1030 kg and
= 2 ×
1030 kg and
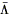 52 is the
cosmological constant in units of 10-52 m-2.
52 is the
cosmological constant in units of 10-52 m-2.