5. EXAMPLES OF MISLEADING RESULTS INDUCED BY CONVENTIONAL STATISTICS

As already discussed, confidence levels are intuitively thought (and usually taught) as probabilities for the true values. I must recognize that many frequentist books do insist on the fact that the probability statement is not referred to the true value. But then, when these books have to explain the ``real meaning'' of the result, they are forced to use ambiguous sentences which remain stamped in the memory of the reader much more than the frequentistically-correct twisted reasoning that they try to explain. For example Frodesen et al. [13] speak about ``the faith we attach to this statement'', as if ``faith'' was not the same as degree of belief...); Eadie et al. [13] introduce the argument saying that ``we want to find the range ...which contains the true value 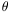_° with probability 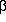'' ⁽¹⁶⁾ ; and so on.

Similarly, significance levels are usually taken as probability of the tested hypothesis. Also this non-orthodox interpretation is stimulated by sentences like ``in statistical context, the words highly significant mean proved beyond a reasonable doubt''. It is also well known that the arbitrary translation of p-values into probability of the null hypothesis produces more severe mistakes than those concerning the use of confidence interval for uncertainty statements on true values.

Let us consider some real life examples of the misinterpretation of the two kinds just described.

5.1. Claims of new physics based on p-values

You may have heard in past years some rumors, or even official claims, of discoveries of ``New Physics'', i.e. of phenomenology which goes behind the so called Standard Model of elementary particles. Then, after some time, these announcements were systematically recognized as having been false alarms, with a consequent reduction in the credibility of the HEP community in the eyes of public opinion and tax payers (with easily imaginable long term aftermath for government support of this research). All these fake discoveries were based on considering low p-values as probability of the null hypothesis ``no new effect''. The most recent example of this kind is the so called 1997 ``HERA high Q<sup>2</sup> events excess''. The H1 and ZEUS collaborations, analyzing data collected at the HERA very high energy electron-proton collider in Hamburg (Germany), found an excess of events (with respect to expectations) in the kinematical region corresponding to very hard interactions [19]. The ``combined significance'' ⁽¹⁷⁾ of the excess was of the order of 1%. Its interpretation as a hint of new physics was even suggested by official statement by the laboratory and by other agencies. For example the DESY official statement was ``...the joint distribution has a probability of less than one percent to come from Standard Model NC DIS processes'' [22] (then it implies ``it has a > 99% probability of not coming from the standard model!'' ⁽¹⁸⁾ ). Similarly, the Italian INFN reported that ``la probabilità che gli eventi osservati siano una fluttazione statistica è inferiore all'1%'' (then, it implies that ``with 99% probability, the events are not a statistical fluctuation, i.e. new physics''!). This is the reason why the press reported the news as ``scientists are practically sure they have found new physics''. What I found astonishing is that most of the people I talked to had real difficulty in understanding that this probability inversion is not legitimate. Only when I forced them to state their degree of belief using the logic of the coherent bet did it emerge that most of my colleagues would not even place a 1:1 bet in favour of the new discovery. Nevertheless, they were in favour of publishing the result because the loss function was absolutely unbalanced (an indirect Nobel prize against essentially nothing).

5.2. What does a lower mass bound mean?

The second example concerns confidence intervals, and it comes from new particle search. This has always been one of the main activities of HEP. New particles are postulated by theories and experimentalists look for evidence for them in experimental data. Usually, if the particle is not ``observed'' <sup>(19)</sup> one says that, although the observation does not disprove the existence of the particle, this is an indication of the fact that the particle is ``too heavy''. The result is then quantified by a ``lower bound'' at a ``95% confidence level''. Without entering into detail of how the limit is operationally defined (see, e.g., [24] and references therein, in particular [25], to have an idea of the level of complication reachable to solve a simple problem), I want to point out that also in this case the result can be misleading. Again I will give a real life example. A combined analysis of all the LEP experiments on the Higgs mass concluded recently that ``A 95% confidence level lower bound of 77.5 GeV/c<sup>2</sup> is obtained for the mass of the Standard Model Higgs boson'' <sup>(20)</sup> . This sounds as if one were sure at 95% that the mass is above the quoted bound. In fact, most of the people I interviewed about the meaning of the statement, even those belonging to the LEP experimental teams, answered ``if the Higgs boson exists at all, then there is 95% probability that its mass is above the limit''. There were also a few people who answered ``if I do a MC simulation of the decay of a 77.5 GeV Higgs boson, I get in only 5% of the cases the simulation describing the data'', or ``if there is an Higgs boson and its mass is less than 77.5 GeV, then the observations of the search experiments have a probability of at most 5% of being correct'', or something similar. From all of which it is very difficult to understand, from a logical point of view, why one should be 95% confident that the mass is higher than the bound ⁽²¹⁾ .

The problem can be solved easily with Bayesian methods (see [7] for details). Assuming a flat prior for the mass, one finds that the value of the lower bound is more or less the published one, but only under the condition that the mass does not exceed the kinematical limit of the studied reaction. But this limit is just a few GeV above the stated lower bound. Thus in order to obtain the correct result one needs to renormalize the probability taking account of the possible range of masses above the kinematical limit and for which the experiment has no sensitivity. For this reason, in the case of [24] the probability that the mass value is above 77.5 GeV/c² may easily become 99.9%, or more, depending on the order of magnitude of a possible upper bound for the mass. Then, in practice these lower bounds can be taken as certainties ⁽²²⁾ .

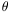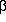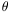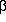¹⁶ I think that Aristoteles would have gotten mad if somebody had tried to convince him that the proposition ``the range contains <sub>°</sub> with probability '' does not imply ``_° is in that range with probability ''. Back.

¹⁷ Physicists are not familiar with the term p-value (readers not familiar with this term may find a concise review in [20]). Moreover, they are usually not aware of the implications of the fact that the statistical significance takes into account also the probability of unobserved data (see, e.g., [21]). Back.

¹⁸ One might think that the misleading meaning of that sentence was due to unfortunate wording, but this possibility is ruled out by other statements which show clearly a quite odd point of view of probabilistic matter. In fact the DESY 1998 activity report [23] insists in saying that ``the likelihood that the data produced is the result of a statistical fluctuation, ..., is equivalent to that of tossing a coin and throwing seven 'heads' or 'tails' in a row'' (replacing 'probability' by 'likelihood' does not change the sense of the message). Then, trying to explain the meaning of a statistical fluctuation, the following example is given: ``This process can be simulated with a die. If the number of times a die is thrown is sufficiently large, the die falls equally often on all faces, i.e. all six numbers occur equally often. The probability for each face is exactly a sixth or 16.66% - assuming the die is not loaded. If the die is thrown less often, then the probability curve for the distribution of the six die values is no longer a straight line but has peaks and troughs. The probability distribution obtained by throwing the die varies about the theoretical value of 16.66% depending on how many times it is thrown''. Back.

¹⁹ This concept of ``observation'' is not like that of seeing a black swan, to mention a famous classical example. New particles leave signatures in the detector that on an event by event basis cannot be distinguished by other processes (background). A statistical (inferential) analysis is therefore needed. Back.

²⁰ In the meanwhile new data have increased this limit, but the actual number is irrelevant for this discussion. Back.

²¹ There was also somebody who refused to answer because ``your question is going to be difficult to answer'', or without any justification (perhaps they realized that it was impossible to explain the statement to a scientific journalist, or to a government authority - these were the terms of my question - without using probabilistic statements which were incompatible with what they thought about probability). Back.

²² There are in fact theorists who ``assume'' the lower bounds as certain bounds in their considerations. Perhaps they do it intuitively, or because they have heard in the last decades of thousands of these 95% lower bounds, and never a particle has then shown up in the 5% side... Back.