Next Contents Previous

4. GRAVITATION

Having paid our mathematical dues, we are now prepared to examine the physics of gravitation as described by general relativity. This subject falls naturally into two pieces: how the curvature of spacetime acts on matter to manifest itself as "gravity", and how energy and momentum influence spacetime to create curvature. In either case it would be legitimate to start at the top, by stating outright the laws governing physics in curved spacetime and working out their consequences. Instead, we will try to be a little more motivational, starting with basic physical principles and attempting to argue that these lead naturally to an almost unique physical theory.

The most basic of these physical principles is the Principle of Equivalence, which comes in a variety of forms. The earliest form dates from Galileo and Newton, and is known as the Weak Equivalence Principle, or WEP. The WEP states that the "inertial mass" and "gravitational mass" of any object are equal. To see what this means, think about Newton's Second Law. This relates the force exerted on an object to the acceleration it undergoes, setting them proportional to each other with the constant of proportionality being the inertial mass mi:

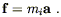
Equation 4.1 (4.1)

The inertial mass clearly has a universal character, related to the resistance you feel when you try to push on the object; it is the same constant no matter what kind of force is being exerted. We also have the law of gravitation, which states that the gravitational force exerted on an object is proportional to the gradient of a scalar field $ \Phi$, known as the gravitational potential. The constant of proportionality in this case is called the gravitational mass mg:

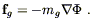
Equation 4.2 (4.2)

On the face of it, mg has a very different character than mi; it is a quantity specific to the gravitational force. If you like, it is the "gravitational charge" of the body. Nevertheless, Galileo long ago showed (apocryphally by dropping weights off of the Leaning Tower of Pisa, actually by rolling balls down inclined planes) that the response of matter to gravitation was universal - every object falls at the same rate in a gravitational field, independent of the composition of the object. In Newtonian mechanics this translates into the WEP, which is simply

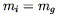
Equation 4.3 (4.3)

for any object. An immediate consequence is that the behavior of freely-falling test particles is universal, independent of their mass (or any other qualities they may have); in fact we have

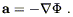
Equation 4.4 (4.4)

The universality of gravitation, as implied by the WEP, can be stated in another, more popular, form. Imagine that we consider a physicist in a tightly sealed box, unable to observe the outside world, who is doing experiments involving the motion of test particles, for example to measure the local gravitational field. Of course she would obtain different answers if the box were sitting on the moon or on Jupiter than she would on the Earth. But the answers would also be different if the box were accelerating at a constant velocity; this would change the acceleration of the freely-falling particles with respect to the box. The WEP implies that there is no way to disentangle the effects of a gravitational field from those of being in a uniformly accelerating frame, simply by observing the behavior of freely-falling particles. This follows from the universality of gravitation; it would be possible to distinguish between uniform acceleration and an electromagnetic field, by observing the behavior of particles with different charges. But with gravity it is impossible, since the "charge" is necessarily proportional to the (inertial) mass.

To be careful, we should limit our claims about the impossibility of distinguishing gravity from uniform acceleration by restricting our attention to "small enough regions of spacetime." If the sealed box were sufficiently big, the gravitational field would change from place to place in an observable way, while the effect of acceleration is always in the same direction. In a rocket ship or elevator, the particles always fall straight down:

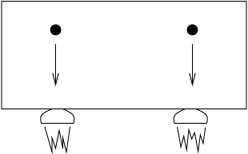
Figure 4.1

In a very big box in a gravitational field, however, the particles will move toward the center of the Earth (for example), which might be a different direction in different regions:

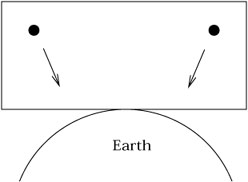
Figure 4.2

The WEP can therefore be stated as "the laws of freely-falling particles are the same in a gravitational field and a uniformly accelerated frame, in small enough regions of spacetime." In larger regions of spacetime there will be inhomogeneities in the gravitational field, which will lead to tidal forces which can be detected.

After the advent of special relativity, the concept of mass lost some of its uniqueness, as it became clear that mass was simply a manifestation of energy and momentum (E = mc2 and all that). It was therefore natural for Einstein to think about generalizing the WEP to something more inclusive. His idea was simply that there should be no way whatsoever for the physicist in the box to distinguish between uniform acceleration and an external gravitational field, no matter what experiments she did (not only by dropping test particles). This reasonable extrapolation became what is now known as the Einstein Equivalence Principle, or EEP: "In small enough regions of spacetime, the laws of physics reduce to those of special relativity; it is impossible to detect the existence of a gravitational field."

In fact, it is hard to imagine theories which respect the WEP but violate the EEP. Consider a hydrogen atom, a bound state of a proton and an electron. Its mass is actually less than the sum of the masses of the proton and electron considered individually, because there is a negative binding energy - you have to put energy into the atom to separate the proton and electron. According to the WEP, the gravitational mass of the hydrogen atom is therefore less than the sum of the masses of its constituents; the gravitational field couples to electromagnetism (which holds the atom together) in exactly the right way to make the gravitational mass come out right. This means that not only must gravity couple to rest mass universally, but to all forms of energy and momentum - which is practically the claim of the EEP. It is possible to come up with counterexamples, however; for example, we could imagine a theory of gravity in which freely falling particles began to rotate as they moved through a gravitational field. Then they could fall along the same paths as they would in an accelerated frame (thereby satisfying the WEP), but you could nevertheless detect the existence of the gravitational field (in violation of the EEP). Such theories seem contrived, but there is no law of nature which forbids them.

Sometimes a distinction is drawn between "gravitational laws of physics" and "non-gravitational laws of physics," and the EEP is defined to apply only to the latter. Then one defines the "Strong Equivalence Principle" (SEP) to include all of the laws of physics, gravitational and otherwise. I don't find this a particularly useful distinction, and won't belabor it. For our purposes, the EEP (or simply "the principle of equivalence") includes all of the laws of physics.

It is the EEP which implies (or at least suggests) that we should attribute the action of gravity to the curvature of spacetime. Remember that in special relativity a prominent role is played by inertial frames - while it was not possible to single out some frame of reference as uniquely "at rest", it was possible to single out a family of frames which were "unaccelerated" (inertial). The acceleration of a charged particle in an electromagnetic field was therefore uniquely defined with respect to these frames. The EEP, on the other hand, implies that gravity is inescapable - there is no such thing as a "gravitationally neutral object" with respect to which we can measure the acceleration due to gravity. It follows that "the acceleration due to gravity" is not something which can be reliably defined, and therefore is of little use.

Instead, it makes more sense to define "unaccelerated" as "freely falling," and that is what we shall do. This point of view is the origin of the idea that gravity is not a "force" - a force is something which leads to acceleration, and our definition of zero acceleration is "moving freely in the presence of whatever gravitational field happens to be around."

This seemingly innocuous step has profound implications for the nature of spacetime. In SR, we had a procedure for starting at some point and constructing an inertial frame which stretched throughout spacetime, by joining together rigid rods and attaching clocks to them. But, again due to inhomogeneities in the gravitational field, this is no longer possible. If we start in some freely-falling state and build a large structure out of rigid rods, at some distance away freely-falling objects will look like they are "accelerating" with respect to this reference frame, as shown in the figure on the next page.

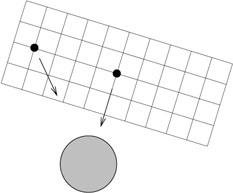
Figure 4.3

The solution is to retain the notion of inertial frames, but to discard the hope that they can be uniquely extended throughout space and time. Instead we can define locally inertial frames, those which follow the motion of freely falling particles in small enough regions of spacetime. (Every time we say "small enough regions", purists should imagine a limiting procedure in which we take the appropriate spacetime volume to zero.) This is the best we can do, but it forces us to give up a good deal. For example, we can no longer speak with confidence about the relative velocity of far away objects, since the inertial reference frames appropriate to those objects are independent of those appropriate to us.

So far we have been talking strictly about physics, without jumping to the conclusion that spacetime should be described as a curved manifold. It should be clear, however, why such a conclusion is appropriate. The idea that the laws of special relativity should be obeyed in sufficiently small regions of spacetime, and further that local inertial frames can be established in such regions, corresponds to our ability to construct Riemann normal coordinates at any one point on a manifold - coordinates in which the metric takes its canonical form and the Christoffel symbols vanish. The impossibility of comparing velocities (vectors) at widely separated regions corresponds to the path-dependence of parallel transport on a curved manifold. These considerations were enough to give Einstein the idea that gravity was a manifestation of spacetime curvature. But in fact we can be even more persuasive. (It is impossible to "prove" that gravity should be thought of as spacetime curvature, since scientific hypotheses can only be falsified, never verified [and not even really falsified, as Thomas Kuhn has famously argued]. But there is nothing to be dissatisfied with about convincing plausibility arguments, if they lead to empirically successful theories.)

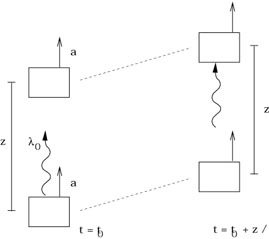
Let's consider one of the celebrated predictions of the EEP, the gravitational redshift. Consider two boxes, a distance z apart, moving (far away from any matter, so we assume in the absence of any gravitational field) with some constant acceleration a. At time t0 the trailing box emits a photon of wavelength $ \lambda_{0}^{}$.

Figure 4.4

The boxes remain a constant distance apart, so the photon reaches the leading box after a time $ \Delta$t = z/c in the reference frame of the boxes. In this time the boxes will have picked up an additional velocity $ \Delta$v = a$ \Delta$t = az/c. Therefore, the photon reaching the lead box will be redshifted by the conventional Doppler effect by an amount

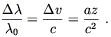
Equation 4.5 (4.5)

(We assume $ \Delta$v/c is small, so we only work to first order.) According to the EEP, the same thing should happen in a uniform gravitational field. So we imagine a tower of height z sitting on the surface of a planet, with ag the strength of the gravitational field (what Newton would have called the "acceleration due to gravity").

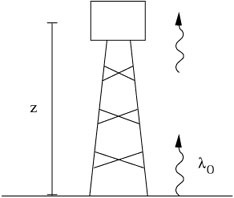
Figure 4.5

This situation is supposed to be indistinguishable from the previous one, from the point of view of an observer in a box at the top of the tower (able to detect the emitted photon, but otherwise unable to look outside the box). Therefore, a photon emitted from the ground with wavelength $ \lambda_{0}^{}$ should be redshifted by an amount

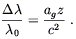
Equation 4.6 (4.6)

This is the famous gravitational redshift. Notice that it is a direct consequence of the EEP, not of the details of general relativity. It has been verified experimentally, first by Pound and Rebka in 1960. They used the Mössbauer effect to measure the change in frequency in $ \gamma$-rays as they traveled from the ground to the top of Jefferson Labs at Harvard.

The formula for the redshift is more often stated in terms of the Newtonian potential $ \Phi$, where $ \bf a_{g}^{}$ = $ \nabla$$ \Phi$. (The sign is changed with respect to the usual convention, since we are thinking of $ \bf a_{g}^{}$ as the acceleration of the reference frame, not of a particle with respect to this reference frame.) A non-constant gradient of $ \Phi$ is like a time-varying acceleration, and the equivalent net velocity is given by integrating over the time between emission and absorption of the photon. We then have

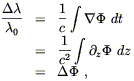
Equation 4.7 (4.7)

where $ \Delta$$ \Phi$ is the total change in the gravitational potential, and we have once again set c = 1. This simple formula for the gravitational redshift continues to be true in more general circumstances. Of course, by using the Newtonian potential at all, we are restricting our domain of validity to weak gravitational fields, but that is usually completely justified for observable effects.

The gravitational redshift leads to another argument that we should consider spacetime as curved. Consider the same experimental setup that we had before, now portrayed on the spacetime diagram on the next page.

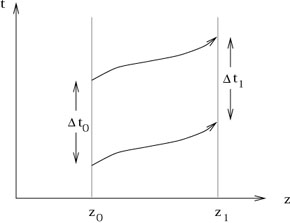
Figure 4.6

The physicist on the ground emits a beam of light with wavelength $ \lambda_{0}^{}$ from a height z0, which travels to the top of the tower at height z1. The time between when the beginning of any single wavelength of the light is emitted and the end of that same wavelength is emitted is $ \Delta$t0 = $ \lambda_{0}^{}$/c, and the same time interval for the absorption is $ \Delta$t1 = $ \lambda_{1}^{}$/c. Since we imagine that the gravitational field is not varying with time, the paths through spacetime followed by the leading and trailing edge of the single wave must be precisely congruent. (They are represented by some generic curved paths, since we do not pretend that we know just what the paths will be.) Simple geometry tells us that the times $ \Delta$t0 and $ \Delta$t1 must be the same. But of course they are not; the gravitational redshift implies that $ \Delta$t1 > $ \Delta$t0. (Which we can interpret as "the clock on the tower appears to run more quickly.") The fault lies with "simple geometry"; a better description of what happens is to imagine that spacetime is curved.

All of this should constitute more than enough motivation for our claim that, in the presence of gravity, spacetime should be thought of as a curved manifold. Let us now take this to be true and begin to set up how physics works in a curved spacetime. The principle of equivalence tells us that the laws of physics, in small enough regions of spacetime, look like those of special relativity. We interpret this in the language of manifolds as the statement that these laws, when written in Riemannian normal coordinates x$\scriptstyle \mu$ based at some point p, are described by equations which take the same form as they would in flat space. The simplest example is that of freely-falling (unaccelerated) particles. In flat space such particles move in straight lines; in equations, this is expressed as the vanishing of the second derivative of the parameterized path x$\scriptstyle \mu$($ \lambda$):

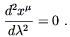
Equation 4.8 (4.8)

According to the EEP, exactly this equation should hold in curved space, as long as the coordinates x$\scriptstyle \mu$ are RNC's. What about some other coordinate system? As it stands, (4.8) is not an equation between tensors. However, there is a unique tensorial equation which reduces to (4.8) when the Christoffel symbols vanish; it is

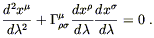
Equation 4.9 (4.9)

Of course, this is simply the geodesic equation. In general relativity, therefore, free particles move along geodesics; we have mentioned this before, but now you know why it is true.

As far as free particles go, we have argued that curvature of spacetime is necessary to describe gravity; we have not yet shown that it is sufficient. To do so, we can show how the usual results of Newtonian gravity fit into the picture. We define the "Newtonian limit" by three requirements: the particles are moving slowly (with respect to the speed of light), the gravitational field is weak (can be considered a perturbation of flat space), and the field is also static (unchanging with time). Let us see what these assumptions do to the geodesic equation, taking the proper time $ \tau$ as an affine parameter. "Moving slowly" means that

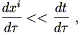
Equation 4.10 (4.10)

so the geodesic equation becomes

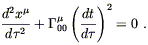
Equation 4.11 (4.11)

Since the field is static, the relevant Christoffel symbols $ \Gamma^{\mu}_{00}$ simplify:

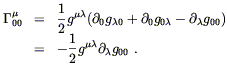
Equation 4.12 (4.12)

Finally, the weakness of the gravitational field allows us to decompose the metric into the Minkowski form plus a small perturbation:

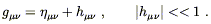
Equation 4.13 (4.13)

(We are working in Cartesian coordinates, so $ \eta_{\mu\nu}^{}$ is the canonical form of the metric. The "smallness condition" on the metric perturbation h$\scriptstyle \mu$$\scriptstyle \nu$ doesn't really make sense in other coordinates.) From the definition of the inverse metric, g$\scriptstyle \mu$$\scriptstyle \nu$g$\scriptstyle \nu$$\scriptstyle \sigma$ = $ \delta^{\mu}_{\sigma}$, we find that to first order in h,

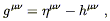
Equation 4.14 (4.14)

where h$\scriptstyle \mu$$\scriptstyle \nu$ = $ \eta^{\mu\rho}_{}$$ \eta^{\nu\sigma}_{}$h$\scriptstyle \rho$$\scriptstyle \sigma$. In fact, we can use the Minkowski metric to raise and lower indices on an object of any definite order in h, since the corrections would only contribute at higher orders.

Putting it all together, we find

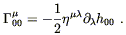
Equation 4.15 (4.15)

The geodesic equation (4.11) is therefore

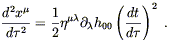
Equation 4.16 (4.16)

Using $ \partial_{0}$h00 = 0, the $ \mu$ = 0 component of this is just

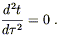
Equation 4.17 (4.17)

That is, $ {{dt}\over{d\tau}}$ is constant. To examine the spacelike components of (4.16), recall that the spacelike components of $ \eta^{\mu\nu}_{}$ are just those of a 3 × 3 identity matrix. We therefore have

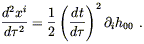
Equation 4.18 (4.18)

Dividing both sides by $ \left(\vphantom{{{d t}\over{d\tau}}}\right.$$ {{dt}\over{d\tau}}$ $ \left.\vphantom{{{d t}\over{d\tau}}}\right)^{2}_{}$ has the effect of converting the derivative on the left-hand side from $ \tau$ to t, leaving us with

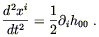
Equation 4.19 (4.19)

This begins to look a great deal like Newton's theory of gravitation. In fact, if we compare this equation to (4.4), we find that they are the same once we identify

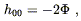
Equation 4.20 (4.20)

or in other words

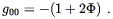
Equation 4.21 (4.21)

Therefore, we have shown that the curvature of spacetime is indeed sufficient to describe gravity in the Newtonian limit, as long as the metric takes the form (4.21). It remains, of course, to find field equations for the metric which imply that this is the form taken, and that for a single gravitating body we recover the Newtonian formula

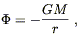
Equation 4.22 (4.22)

but that will come soon enough.

Our next task is to show how the remaining laws of physics, beyond those governing freely-falling particles, adapt to the curvature of spacetime. The procedure essentially follows the paradigm established in arguing that free particles move along geodesics. Take a law of physics in flat space, traditionally written in terms of partial derivatives and the flat metric. According to the equivalence principle this law will hold in the presence of gravity, as long as we are in Riemannian normal coordinates. Translate the law into a relationship between tensors; for example, change partial derivatives to covariant ones. In RNC's this version of the law will reduce to the flat-space one, but tensors are coordinate-independent objects, so the tensorial version must hold in any coordinate system.

This procedure is sometimes given a name, the Principle of Covariance. I'm not sure that it deserves its own name, since it's really a consequence of the EEP plus the requirement that the laws of physics be independent of coordinates. (The requirement that laws of physics be independent of coordinates is essentially impossible to even imagine being untrue. Given some experiment, if one person uses one coordinate system to predict a result and another one uses a different coordinate system, they had better agree.) Another name is the "comma-goes-to-semicolon rule", since at a typographical level the thing you have to do is replace partial derivatives (commas) with covariant ones (semicolons).

We have already implicitly used the principle of covariance (or whatever you want to call it) in deriving the statement that free particles move along geodesics. For the most part, it is very simple to apply it to interesting cases. Consider for example the formula for conservation of energy in flat spacetime, $ \partial_{\mu}$T$\scriptstyle \mu$$\scriptstyle \nu$ = 0. The adaptation to curved spacetime is immediate:

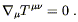
Equation 4.23 (4.23)

This equation expresses the conservation of energy in the presence of a gravitational field.

Unfortunately, life is not always so easy. Consider Maxwell's equations in special relativity, where it would seem that the principle of covariance can be applied in a straightforward way. The inhomogeneous equation $ \partial_{\mu}$F$\scriptstyle \nu$$\scriptstyle \mu$ = 4$ \pi$J$\scriptstyle \nu$ becomes

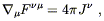
Equation 4.24 (4.24)

and the homogeneous one $ \partial_{[\mu}$F$\scriptstyle \nu$$\scriptstyle \lambda$] = 0 becomes

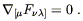
Equation 4.25 (4.25)

On the other hand, we could also write Maxwell's equations in flat space in terms of differential forms as

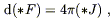
Equation 4.26 (4.26)

and

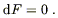
Equation 4.27 (4.27)

These are already in perfectly tensorial form, since we have shown that the exterior derivative is a well-defined tensor operator regardless of what the connection is. We therefore begin to worry a little bit; what is the guarantee that the process of writing a law of physics in tensorial form gives a unique answer? In fact, as we have mentioned earlier, the differential forms versions of Maxwell's equations should be taken as fundamental. Nevertheless, in this case it happens to make no difference, since in the absence of torsion (4.26) is identical to (4.24), and (4.27) is identical to (4.25); the symmetric part of the connection doesn't contribute. Similarly, the definition of the field strength tensor in terms of the potential A$\scriptstyle \mu$ can be written either as

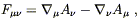
Equation 4.28 (4.28)

or equally well as

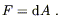
Equation 4.29 (4.29)

The worry about uniqueness is a real one, however. Imagine that two vector fields X$\scriptstyle \mu$ and Y$\scriptstyle \nu$ obey a law in flat space given by

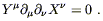
Equation 4.30 (4.30)

The problem in writing this as a tensor equation should be clear: the partial derivatives can be commuted, but covariant derivatives cannot. If we simply replace the partials in (4.30) by covariant derivatives, we get a different answer than we would if we had first exchanged the order of the derivatives (leaving the equation in flat space invariant) and then replaced them. The difference is given by

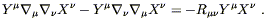
Equation 4.31 (4.31)

The prescription for generalizing laws from flat to curved spacetimes does not guide us in choosing the order of the derivatives, and therefore is ambiguous about whether a term such as that in (4.31) should appear in the presence of gravity. (The problem of ordering covariant derivatives is similar to the problem of operator-ordering ambiguities in quantum mechanics.)

In the literature you can find various prescriptions for dealing with ambiguities such as this, most of which are sensible pieces of advice such as remembering to preserve gauge invariance for electromagnetism. But deep down the real answer is that there is no way to resolve these problems by pure thought alone; the fact is that there may be more than one way to adapt a law of physics to curved space, and ultimately only experiment can decide between the alternatives.

In fact, let us be honest about the principle of equivalence: it serves as a useful guideline, but it does not deserve to be treated as a fundamental principle of nature. From the modern point of view, we do not expect the EEP to be rigorously true. Consider the following alternative version of (4.24):

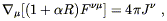
Equation 4.32 (4.32)

where R is the Ricci scalar and $ \alpha$ is some coupling constant. If this equation correctly described electrodynamics in curved spacetime, it would be possible to measure R even in an arbitrarily small region, by doing experiments with charged particles. The equivalence principle therefore demands that $ \alpha$ = 0. But otherwise this is a perfectly respectable equation, consistent with charge conservation and other desirable features of electromagnetism, which reduces to the usual equation in flat space. Indeed, in a world governed by quantum mechanics we expect all possible couplings between different fields (such as gravity and electromagnetism) that are consistent with the symmetries of the theory (in this case, gauge invariance). So why is it reasonable to set $ \alpha$ = 0? The real reason is one of scales. Notice that the Ricci tensor involves second derivatives of the metric, which is dimensionless, so R has dimensions of (length)-2 (with c = 1). Therefore $ \alpha$ must have dimensions of (length)2. But since the coupling represented by $ \alpha$ is of gravitational origin, the only reasonable expectation for the relevant length scale is

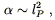
Equation 4.33 (4.33)

where lP is the Planck length

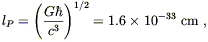
Equation 4.34 (4.34)

where $ \hbar$ is of course Planck's constant. So the length scale corresponding to this coupling is extremely small, and for any conceivable experiment we expect the typical scale of variation for the gravitational field to be much larger. Therefore the reason why this equivalence-principle-violating term can be safely ignored is simply because $ \alpha$R is probably a fantastically small number, far out of the reach of any experiment. On the other hand, we might as well keep an open mind, since our expectations are not always borne out by observation.

Having established how physical laws govern the behavior of fields and objects in a curved spacetime, we can complete the establishment of general relativity proper by introducing Einstein's field equations, which govern how the metric responds to energy and momentum. We will actually do this in two ways: first by an informal argument close to what Einstein himself was thinking, and then by starting with an action and deriving the corresponding equations of motion.

The informal argument begins with the realization that we would like to find an equation which supersedes the Poisson equation for the Newtonian potential:

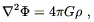
Equation 4.35 (4.35)

where $ \nabla^{2}_{}$ = $ \delta^{ij}_{}$$ \partial_{i}$$ \partial_{j}$ is the Laplacian in space and $ \rho$ is the mass density. (The explicit form of $ \Phi$ given in (4.22) is one solution of (4.35), for the case of a pointlike mass distribution.) What characteristics should our sought-after equation possess? On the left-hand side of (4.35) we have a second-order differential operator acting on the gravitational potential, and on the right-hand side a measure of the mass distribution. A relativistic generalization should take the form of an equation between tensors. We know what the tensor generalization of the mass density is; it's the energy-momentum tensor T$\scriptstyle \mu$$\scriptstyle \nu$. The gravitational potential, meanwhile, should get replaced by the metric tensor. We might therefore guess that our new equation will have T$\scriptstyle \mu$$\scriptstyle \nu$ set proportional to some tensor which is second-order in derivatives of the metric. In fact, using (4.21) for the metric in the Newtonian limit and T00 = $ \rho$, we see that in this limit we are looking for an equation that predicts

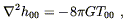
Equation 4.36 (4.36)

but of course we want it to be completely tensorial.

The left-hand side of (4.36) does not obviously generalize to a tensor. The first choice might be to act the D'Alembertian $ \Box$ = $ \nabla^{\mu}_{}$$ \nabla_{\mu}^{}$ on the metric g$\scriptstyle \mu$$\scriptstyle \nu$, but this is automatically zero by metric compatibility. Fortunately, there is an obvious quantity which is not zero and is constructed from second derivatives (and first derivatives) of the metric: the Riemann tensor R$\scriptstyle \rho$$\scriptstyle \sigma$$\scriptstyle \mu$$\scriptstyle \nu$. It doesn't have the right number of indices, but we can contract it to form the Ricci tensor R$\scriptstyle \mu$$\scriptstyle \nu$, which does (and is symmetric to boot). It is therefore reasonable to guess that the gravitational field equations are

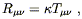
Equation 4.37 (4.37)

for some constant $ \kappa$. In fact, Einstein did suggest this equation at one point. There is a problem, unfortunately, with conservation of energy. According to the Principle of Equivalence, the statement of energy-momentum conservation in curved spacetime should be

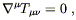
Equation 4.38 (4.38)

which would then imply

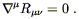
Equation 4.39 (4.39)

This is certainly not true in an arbitrary geometry; we have seen from the Bianchi identity (3.94) that

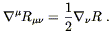
Equation 4.40 (4.40)

But our proposed field equation implies that R = $ \kappa$g$\scriptstyle \mu$$\scriptstyle \nu$T$\scriptstyle \mu$$\scriptstyle \nu$ = $ \kappa$T, so taking these together we have

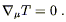
Equation 4.41 (4.41)

The covariant derivative of a scalar is just the partial derivative, so (4.41) is telling us that T is constant throughout spacetime. This is highly implausible, since T = 0 in vacuum while T > 0 in matter. We have to try harder.

(Actually we are cheating slightly, in taking the equation $ \nabla^{\mu}_{}$T$\scriptstyle \mu$$\scriptstyle \nu$ = 0 so seriously. If as we said, the equivalence principle is only an approximate guide, we could imagine that there are nonzero terms on the right-hand side involving the curvature tensor. Later we will be more precise and argue that they are strictly zero.)

Of course we don't have to try much harder, since we already know of a symmetric (0, 2) tensor, constructed from the Ricci tensor, which is automatically conserved: the Einstein tensor

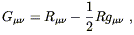
Equation 4.42 (4.42)

which always obeys $ \nabla^{\mu}_{}$G$\scriptstyle \mu$$\scriptstyle \nu$ = 0. We are therefore led to propose

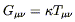
Equation 4.43 (4.43)

as a field equation for the metric. This equation satisfies all of the obvious requirements; the right-hand side is a covariant expression of the energy and momentum density in the form of a symmetric and conserved (0, 2) tensor, while the left-hand side is a symmetric and conserved (0, 2) tensor constructed from the metric and its first and second derivatives. It only remains to see whether it actually reproduces gravity as we know it.

To answer this, note that contracting both sides of (4.43) yields (in four dimensions)

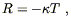
Equation 4.44 (4.44)

and using this we can rewrite (4.43) as

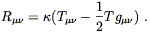
Equation 4.45 (4.45)

This is the same equation, just written slightly differently. We would like to see if it predicts Newtonian gravity in the weak-field, time-independent, slowly-moving-particles limit. In this limit the rest energy $ \rho$ = T00 will be much larger than the other terms in T$\scriptstyle \mu$$\scriptstyle \nu$, so we want to focus on the $ \mu$ = 0, $ \nu$ = 0 component of (4.45). In the weak-field limit, we write (in accordance with (4.13) and (4.14))

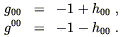
Equation 4.46 (4.46)

The trace of the energy-momentum tensor, to lowest nontrivial order, is

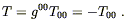
Equation 4.47 (4.47)

Plugging this into (4.45), we get

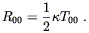
Equation 4.48 (4.48)

This is an equation relating derivatives of the metric to the energy density. To find the explicit expression in terms of the metric, we need to evaluate R00 = R$\scriptstyle \lambda$0$\scriptstyle \lambda$ 0. In fact we only need Ri0i0, since R0000 = 0. We have

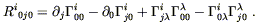
Equation 4.49 (4.49)

The second term here is a time derivative, which vanishes for static fields. The third and fourth terms are of the form ($ \Gamma$)2, and since $ \Gamma$ is first-order in the metric perturbation these contribute only at second order, and can be neglected. We are left with Ri0j0 = $ \partial_{j}$$ \Gamma^{i}_{00}$. From this we get

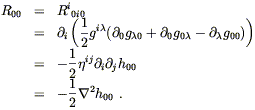
Equation 4.50 (4.50)

Comparing to (4.48), we see that the 00 component of (4.43) in the Newtonian limit predicts

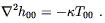
Equation 4.51 (4.51)

But this is exactly (4.36), if we set $ \kappa$ = 8$ \pi$G.

So our guess seems to have worked out. With the normalization fixed by comparison with the Newtonian limit, we can present Einstein's equations for general relativity:

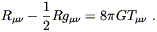
Equation 4.52 (4.52)

These tell us how the curvature of spacetime reacts to the presence of energy-momentum. Einstein, you may have heard, thought that the left-hand side was nice and geometrical, while the right-hand side was somewhat less compelling.

Einstein's equations may be thought of as second-order differential equations for the metric tensor field g$\scriptstyle \mu$$\scriptstyle \nu$. There are ten independent equations (since both sides are symmetric two-index tensors), which seems to be exactly right for the ten unknown functions of the metric components. However, the Bianchi identity $ \nabla^{\mu}_{}$G$\scriptstyle \mu$$\scriptstyle \nu$ = 0 represents four constraints on the functions R$\scriptstyle \mu$$\scriptstyle \nu$, so there are only six truly independent equations in (4.52). In fact this is appropriate, since if a metric is a solution to Einstein's equation in one coordinate system x$\scriptstyle \mu$ it should also be a solution in any other coordinate system x$\scriptstyle \mu{^\prime}$. This means that there are four unphysical degrees of freedom in g$\scriptstyle \mu$$\scriptstyle \nu$ (represented by the four functions x$\scriptstyle \mu{^\prime}$(x$\scriptstyle \mu$)), and we should expect that Einstein's equations only constrain the six coordinate-independent degrees of freedom.

As differential equations, these are extremely complicated; the Ricci scalar and tensor are contractions of the Riemann tensor, which involves derivatives and products of the Christoffel symbols, which in turn involve the inverse metric and derivatives of the metric. Furthermore, the energy-momentum tensor T$\scriptstyle \mu$$\scriptstyle \nu$ will generally involve the metric as well. The equations are also nonlinear, so that two known solutions cannot be superposed to find a third. It is therefore very difficult to solve Einstein's equations in any sort of generality, and it is usually necessary to make some simplifying assumptions. Even in vacuum, where we set the energy-momentum tensor to zero, the resulting equations (from (4.45))

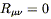
Equation 4.53 (4.53)

can be very difficult to solve. The most popular sort of simplifying assumption is that the metric has a significant degree of symmetry, and we will talk later on about how symmetries of the metric make life easier.

The nonlinearity of general relativity is worth remarking on. In Newtonian gravity the potential due to two point masses is simply the sum of the potentials for each mass, but clearly this does not carry over to general relativity (outside the weak-field limit). There is a physical reason for this, namely that in GR the gravitational field couples to itself. This can be thought of as a consequence of the equivalence principle - if gravitation did not couple to itself, a "gravitational atom" (two particles bound by their mutual gravitational attraction) would have a different inertial mass (due to the negative binding energy) than gravitational mass. From a particle physics point of view this can be expressed in terms of Feynman diagrams. The electromagnetic interaction between two electrons can be thought of as due to exchange of a virtual photon:

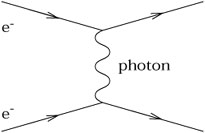
Figure 4.7

But there is no diagram in which two photons exchange another photon between themselves; electromagnetism is linear. The gravitational interaction, meanwhile, can be thought of as due to exchange of a virtual graviton (a quantized perturbation of the metric). The nonlinearity manifests itself as the fact that both electrons and gravitons (and anything else) can exchange virtual gravitons, and therefore exert a gravitational force:

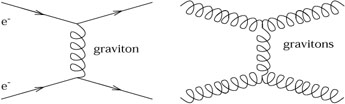
Figure 4.8

There is nothing profound about this feature of gravity; it is shared by most gauge theories, such as quantum chromodynamics, the theory of the strong interactions. (Electromagnetism is actually the exception; the linearity can be traced to the fact that the relevant gauge group, U(1), is abelian.) But it does represent a departure from the Newtonian theory. (Of course this quantum mechanical language of Feynman diagrams is somewhat inappropriate for GR, which has not [yet] been successfully quantized, but the diagrams are just a convenient shorthand for remembering what interactions exist in the theory.)

To increase your confidence that Einstein's equations as we have derived them are indeed the correct field equations for the metric, let's see how they can be derived from a more modern viewpoint, starting from an action principle. (In fact the equations were first derived by Hilbert, not Einstein, and Hilbert did it using the action principle. But he had been inspired by Einstein's previous papers on the subject, and Einstein himself derived the equations independently, so they are rightly named after Einstein. The action, however, is rightly called the Hilbert action.) The action should be the integral over spacetime of a Lagrange density ("Lagrangian" for short, although strictly speaking the Lagrangian is the integral over space of the Lagrange density):

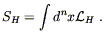
Equation 4.54 (4.54)

The Lagrange density is a tensor density, which can be written as $ \sqrt{-g}$ times a scalar. What scalars can we make out of the metric? Since we know that the metric can be set equal to its canonical form and its first derivatives set to zero at any one point, any nontrivial scalar must involve at least second derivatives of the metric. The Riemann tensor is of course made from second derivatives of the metric, and we argued earlier that the only independent scalar we could construct from the Riemann tensor was the Ricci scalar R. What we did not show, but is nevertheless true, is that any nontrivial tensor made from the metric and its first and second derivatives can be expressed in terms of the metric and the Riemann tensor. Therefore, the only independent scalar constructed from the metric, which is no higher than second order in its derivatives, is the Ricci scalar. Hilbert figured that this was therefore the simplest possible choice for a Lagrangian, and proposed

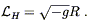
Equation 4.55 (4.55)

The equations of motion should come from varying the action with respect to the metric. In fact let us consider variations with respect to the inverse metric g$\scriptstyle \mu$$\scriptstyle \nu$, which are slightly easier but give an equivalent set of equations. Using R = g$\scriptstyle \mu$$\scriptstyle \nu$R$\scriptstyle \mu$$\scriptstyle \nu$, in general we will have

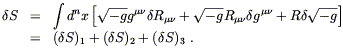
Equation 4.56 (4.56)

The second term ($ \delta$S)2 is already in the form of some expression times $ \delta$g$\scriptstyle \mu$$\scriptstyle \nu$; let's examine the others more closely.

Recall that the Ricci tensor is the contraction of the Riemann tensor, which is given by

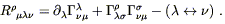
Equation 4.57 (4.57)

The variation of this with respect the metric can be found first varying the connection with respect to the metric, and then substituting into this expression. Let us however consider arbitrary variations of the connection, by replacing

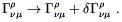
Equation 4.58 (4.58)

The variation $ \delta$$ \Gamma^{\rho}_{\nu\mu}$ is the difference of two connections, and therefore is itself a tensor. We can thus take its covariant derivative,

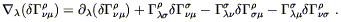
Equation 4.59 (4.59)

Given this expression (and a small amount of labor) it is easy to show that

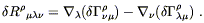
Equation 4.60 (4.60)

You can check this yourself. Therefore, the contribution of the first term in (4.56) to $ \delta$S can be written

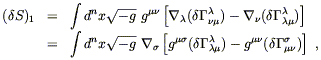
Equation 4.61 (4.61)

where we have used metric compatibility and relabeled some dummy indices. But now we have the integral with respect to the natural volume element of the covariant divergence of a vector; by Stokes's theorem, this is equal to a boundary contribution at infinity which we can set to zero by making the variation vanish at infinity. (We haven't actually shown that Stokes's theorem, as mentioned earlier in terms of differential forms, can be thought of this way, but you can easily convince yourself it's true.) Therefore this term contributes nothing to the total variation.

To make sense of the ($ \delta$S)3 term we need to use the following fact, true for any matrix M:

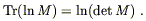
Equation 4.62 (4.62)

Here, ln M is defined by exp(ln M) = M. (For numbers this is obvious, for matrices it's a little less straightforward.) The variation of this identity yields

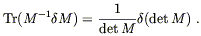
Equation 4.63 (4.63)

Here we have used the cyclic property of the trace to allow us to ignore the fact that M-1 and $ \delta$M may not commute. Now we would like to apply this to the inverse metric, M = g$\scriptstyle \mu$$\scriptstyle \nu$. Then detM = g-1 (where g = detg$\scriptstyle \mu$$\scriptstyle \nu$), and

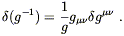
Equation 4.64 (4.64)

Now we can just plug in:

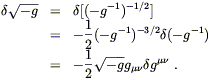
Equation 4.65 (4.65)

Hearkening back to (4.56), and remembering that ($ \delta$S)1 does not contribute, we find

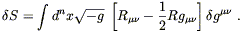
Equation 4.66 (4.66)

This should vanish for arbitrary variations, so we are led to Einstein's equations in vacuum:

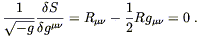
Equation 4.67 (4.67)

The fact that this simple action leads to the same vacuum field equations as we had previously arrived at by more informal arguments certainly reassures us that we are doing something right. What we would really like, however, is to get the non-vacuum field equations as well. That means we consider an action of the form

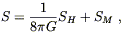
Equation 4.68 (4.68)

where SM is the action for matter, and we have presciently normalized the gravitational action (although the proper normalization is somewhat convention-dependent). Following through the same procedure as above leads to

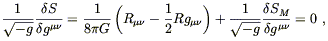
Equation 4.69 (4.69)

and we recover Einstein's equations if we can set

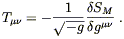
Equation 4.70 (4.70)

What makes us think that we can make such an identification? In fact (4.70) turns out to be the best way to define a symmetric energy-momentum tensor. The tricky part is to show that it is conserved, which is in fact automatically true, but which we will not justify until the next section.

We say that (4.70) provides the "best" definition of the energy-momentum tensor because it is not the only one you will find. In flat Minkowski space, there is an alternative definition which is sometimes given in books on electromagnetism or field theory. In this context energy-momentum conservation arises as a consequence of symmetry of the Lagrangian under spacetime translations. Noether's theorem states that every symmetry of a Lagrangian implies the existence of a conservation law; invariance under the four spacetime translations leads to a tensor S$\scriptstyle \mu$$\scriptstyle \nu$ which obeys $ \partial_{\mu}$S$\scriptstyle \mu$$\scriptstyle \nu$ = 0 (four relations, one for each value of $ \nu$). The details can be found in Wald or in any number of field theory books. Applying Noether's procedure to a Lagrangian which depends on some fields $ \psi^{i}_{}$ and their first derivatives $ \partial_{\mu}$$ \psi^{i}_{}$, we obtain

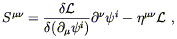
Equation 4.71 (4.71)

where a sum over i is implied. You can check that this tensor is conserved by virtue of the equations of motion of the matter fields. S$\scriptstyle \mu$$\scriptstyle \nu$ often goes by the name "canonical energy-momentum tensor"; however, there are a number of reasons why it is more convenient for us to use (4.70). First and foremost, (4.70) is in fact what appears on the right hand side of Einstein's equations when they are derived from an action, and it is not always possible to generalize (4.71) to curved spacetime. But even in flat space (4.70) has its advantages; it is manifestly symmetric, and also guaranteed to be gauge invariant, neither of which is true for (4.71). We will therefore stick with (4.70) as the definition of the energy-momentum tensor.

Sometimes it is useful to think about Einstein's equations without specifying the theory of matter from which T$\scriptstyle \mu$$\scriptstyle \nu$ is derived. This leaves us with a great deal of arbitrariness; consider for example the question "What metrics obey Einstein's equations?" In the absence of some constraints on T$\scriptstyle \mu$$\scriptstyle \nu$, the answer is "any metric at all"; simply take the metric of your choice, compute the Einstein tensor G$\scriptstyle \mu$$\scriptstyle \nu$ for this metric, and then demand that T$\scriptstyle \mu$$\scriptstyle \nu$ be equal to G$\scriptstyle \mu$$\scriptstyle \nu$. (It will automatically be conserved, by the Bianchi identity.) Our real concern is with the existence of solutions to Einstein's equations in the presence of "realistic" sources of energy and momentum, whatever that means. The most common property that is demanded of T$\scriptstyle \mu$$\scriptstyle \nu$ is that it represent positive energy densities - no negative masses are allowed. In a locally inertial frame this requirement can be stated as $ \rho$ = T00 $ \geq$ 0. To turn this into a coordinate-independent statement, we ask that

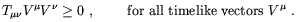
Equation 4.72 (4.72)

This is known as the Weak Energy Condition, or WEC. It seems like a fairly reasonable requirement, and many of the important theorems about solutions to general relativity (such as the singularity theorems of Hawking and Penrose) rely on this condition or something very close to it. Unfortunately it is not set in stone; indeed, it is straightforward to invent otherwise respectable classical field theories which violate the WEC, and almost impossible to invent a quantum field theory which obeys it. Nevertheless, it is legitimate to assume that the WEC holds in all but the most extreme conditions. (There are also stronger energy conditions, but they are even less true than the WEC, and we won't dwell on them.)

We have now justified Einstein's equations in two different ways: as the natural covariant generalization of Poisson's equation for the Newtonian gravitational potential, and as the result of varying the simplest possible action we could invent for the metric. The rest of the course will be an exploration of the consequences of these equations, but before we start on that road let us briefly explore ways in which the equations could be modified. There are an uncountable number of such ways, but we will consider four different possibilities: the introduction of a cosmological constant, higher-order terms in the action, gravitational scalar fields, and a nonvanishing torsion tensor.

The first possibility is the cosmological constant; George Gamow has quoted Einstein as calling this the biggest mistake of his life. Recall that in our search for the simplest possible action for gravity we noted that any nontrivial scalar had to be of at least second order in derivatives of the metric; at lower order all we can create is a constant. Although a constant does not by itself lead to very interesting dynamics, it has an important effect if we add it to the conventional Hilbert action. We therefore consider an action given by

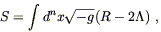
Equation 4.73 (4.73)

where $ \Lambda$ is some constant. The resulting field equations are

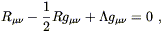
Equation 4.74 (4.74)

and of course there would be an energy-momentum tensor on the right hand side if we had included an action for matter. $ \Lambda$ is the cosmological constant; it was originally introduced by Einstein after it became clear that there were no solutions to his equations representing a static cosmology (a universe unchanging with time on large scales) with a nonzero matter content. If the cosmological constant is tuned just right, it is possible to find a static solution, but it is unstable to small perturbations. Furthermore, once Hubble demonstrated that the universe is expanding, it became less important to find static solutions, and Einstein rejected his suggestion. Like Rasputin, however, the cosmological constant has proven difficult to kill off. If we like we can move the additional term in (4.74) to the right hand side, and think of it as a kind of energy-momentum tensor, with T$\scriptstyle \mu$$\scriptstyle \nu$ = - $ \Lambda$g$\scriptstyle \mu$$\scriptstyle \nu$ (it is automatically conserved by metric compatibility). Then $ \Lambda$ can be interpreted as the "energy density of the vacuum," a source of energy and momentum that is present even in the absence of matter fields. This interpretation is important because quantum field theory predicts that the vacuum should have some sort of energy and momentum. In ordinary quantum mechanics, an harmonic oscillator with frequency $ \omega$ and minimum classical energy E0 = 0 upon quantization has a ground state with energy E0 = $ {1\over 2}$$ \hbar$$ \omega$. A quantized field can be thought of as a collection of an infinite number of harmonic oscillators, and each mode contributes to the ground state energy. The result is of course infinite, and must be appropriately regularized, for example by introducing a cutoff at high frequencies. The final vacuum energy, which is the regularized sum of the energies of the ground state oscillations of all the fields of the theory, has no good reason to be zero and in fact would be expected to have a natural scale

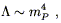
Equation 4.75 (4.75)

where the Planck mass mP is approximately 1019 GeV, or 10-5 grams. Observations of the universe on large scales allow us to constrain the actual value of $ \Lambda$, which turns out to be smaller than (4.75) by at least a factor of 10120. This is the largest known discrepancy between theoretical estimate and observational constraint in physics, and convinces many people that the "cosmological constant problem" is one of the most important unsolved problems today. On the other hand the observations do not tell us that $ \Lambda$ is strictly zero, and in fact allow values that can have important consequences for the evolution of the universe. This mistake of Einstein's therefore continues to bedevil both physicists, who would like to understand why it is so small, and astronomers, who would like to determine whether it is really small enough to be ignored.

A somewhat less intriguing generalization of the Hilbert action would be to include scalars of more than second order in derivatives of the metric. We could imagine an action of the form

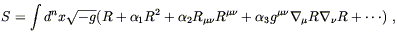
Equation 4.76 (4.76)

where the $ \alpha$'s are coupling constants and the dots represent every other scalar we can make from the curvature tensor, its contractions, and its derivatives. Traditionally, such terms have been neglected on the reasonable grounds that they merely complicate a theory which is already both aesthetically pleasing and empirically successful. However, there are at least three more substantive reasons for this neglect. First, as we shall see below, Einstein's equations lead to a well-posed initial value problem for the metric, in which "coordinates" and "momenta" specified at an initial time can be used to predict future evolution. With higher-derivative terms, we would require not only those data, but also some number of derivatives of the momenta. Second, the main source of dissatisfaction with general relativity on the part of particle physicists is that it cannot be renormalized (as far as we know), and Lagrangians with higher derivatives tend generally to make theories less renormalizable rather than more. Third, by the same arguments we used above when speaking about the limitations of the principle of equivalence, the extra terms in (4.76) should be suppressed (by powers of the Planck mass to some power) relative to the usual Hilbert term, and therefore would not be expected to be of any practical importance to the low-energy world. None of these reasons are completely persuasive, and indeed people continue to consider such theories, but for the most part these models do not attract a great deal of attention.

A set of models which does attract attention are known as scalar-tensor theories of gravity, since they involve both the metric tensor g$\scriptstyle \mu$$\scriptstyle \nu$ and a fundamental scalar field, $ \lambda$. The action can be written

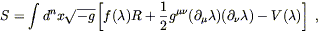
Equation 4.77 (4.77)

where f ($ \lambda$) and V($ \lambda$) are functions which define the theory. Recall from (4.68) that the coefficient of the Ricci scalar in conventional GR is proportional to the inverse of Newton's constant G. In scalar-tensor theories, then, where this coefficient is replaced by some function of a field which can vary throughout spacetime, the "strength" of gravity (as measured by the local value of Newton's constant) will be different from place to place and time to time. In fact the most famous scalar-tensor theory, invented by Brans and Dicke and now named after them, was inspired by a suggestion of Dirac's that the gravitational constant varies with time. Dirac had noticed that there were some interesting numerical coincidences one could discover by taking combinations of cosmological numbers such as the Hubble constant H0 (a measure of the expansion rate of the universe) and typical particle-physics parameters such as the mass of the pion, m$\scriptstyle \pi$. For example,

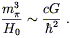
Equation 4.78 (4.78)

If we assume for the moment that this relation is not simply an accident, we are faced with the problem that the Hubble "constant" actually changes with time (in most cosmological models), while the other quantities conventionally do not. Dirac therefore proposed that in fact G varied with time, in such a way as to maintain (4.78); satisfying this proposal was the motivation of Brans and Dicke. These days, experimental test of general relativity are sufficiently precise that we can state with confidence that, if Brans-Dicke theory is correct, the predicted change in G over space and time must be very small, much slower than that necessary to satisfy Dirac's hypothesis. (See Weinberg for details on Brans-Dicke theory and experimental tests.) Nevertheless there is still a great deal of work being done on other kinds of scalar-tensor theories, which turn out to be vital in superstring theory and may have important consequences in the very early universe.

As a final alternative to general relativity, we should mention the possibility that the connection really is not derived from the metric, but in fact has an independent existence as a fundamental field. We will leave it as an exercise for you to show that it is possible to consider the conventional action for general relativity but treat it as a function of both the metric g$\scriptstyle \mu$$\scriptstyle \nu$ and a torsion-free connection $ \Gamma^{\lambda}_{\rho\sigma}$, and the equations of motion derived from varying such an action with respect to the connection imply that $ \Gamma^{\lambda}_{\rho\sigma}$ is actually the Christoffel connection associated with g$\scriptstyle \mu$$\scriptstyle \nu$. We could drop the demand that the connection be torsion-free, in which case the torsion tensor could lead to additional propagating degrees of freedom. Without going into details, the basic reason why such theories do not receive much attention is simply because the torsion is itself a tensor; there is nothing to distinguish it from other, "non-gravitational" tensor fields. Thus, we do not really lose any generality by considering theories of torsion-free connections (which lead to GR) plus any number of tensor fields, which we can name what we like.

With the possibility in mind that one of these alternatives (or, more likely, something we have not yet thought of) is actually realized in nature, for the rest of the course we will work under the assumption that general relativity as based on Einstein's equations or the Hilbert action is the correct theory, and work out its consequences. These consequences, of course, are constituted by the solutions to Einstein's equations for various sources of energy and momentum, and the behavior of test particles in these solutions. Before considering specific solutions in detail, lets look more abstractly at the initial-value problem in general relativity.

In classical Newtonian mechanics, the behavior of a single particle is of course governed by $ \bf f$ = m$ \bf a$. If the particle is moving under the influence of some potential energy field $ \Phi$(x), then the force is $ \bf f$ = - $ \nabla$$ \Phi$, and the particle obeys

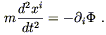
Equation 4.79 (4.79)

This is a second-order differential equation for xi(t), which we can recast as a system of two coupled first-order equations by introducing the momentum $ \bf p$:

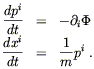
Equation 4.80 (4.80)

The initial-value problem is simply the procedure of specifying a "state" (xi, pi) which serves as a boundary condition with which (4.80) can be uniquely solved. You may think of (4.80) as allowing you, once you are given the coordinates and momenta at some time t, to evolve them forward an infinitesimal amount to a time t + $ \delta$t, and iterate this procedure to obtain the entire solution.

We would like to formulate the analogous problem in general relativity. Einstein's equations G$\scriptstyle \mu$$\scriptstyle \nu$ = 8$ \pi$GT$\scriptstyle \mu$$\scriptstyle \nu$ are of course covariant; they don't single out a preferred notion of "time" through which a state can evolve. Nevertheless, we can by hand pick a spacelike hypersurface (or "slice") $ \Sigma$, specify initial data on that hypersurface, and see if we can evolve uniquely from it to a hypersurface in the future. ("Hyper" because a constant-time slice in four dimensions will be three-dimensional, whereas "surfaces" are conventionally two-dimensional.) This process does violence to the manifest covariance of the theory, but if we are careful we should wind up with a formulation that is equivalent to solving Einstein's equations all at once throughout spacetime.

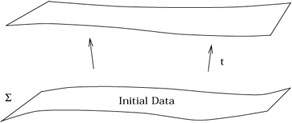
Figure 4.9

Since the metric is the fundamental variable, our first guess is that we should consider the values g$\scriptstyle \mu$$\scriptstyle \nu$|$\scriptstyle \Sigma$ of the metric on our hypersurface to be the "coordinates" and the time derivatives $ \partial_{t}$g$\scriptstyle \mu$$\scriptstyle \nu$|$\scriptstyle \Sigma$ (with respect to some specified time coordinate) to be the "momenta", which together specify the state. (There will also be coordinates and momenta for the matter fields, which we will not consider explicitly.) In fact the equations G$\scriptstyle \mu$$\scriptstyle \nu$ = 8$ \pi$GT$\scriptstyle \mu$$\scriptstyle \nu$ do involve second derivatives of the metric with respect to time (since the connection involves first derivatives of the metric and the Einstein tensor involves first derivatives of the connection), so we seem to be on the right track. However, the Bianchi identity tells us that $ \nabla_{\mu}^{}$G$\scriptstyle \mu$$\scriptstyle \nu$ = 0. We can rewrite this equation as

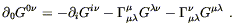
Equation 4.81 (4.81)

A close look at the right hand side reveals that there are no third-order time derivatives; therefore there cannot be any on the left hand side. Thus, although G$\scriptstyle \mu$$\scriptstyle \nu$ as a whole involves second-order time derivatives of the metric, the specific components G0$\scriptstyle \nu$ do not. Of the ten independent components in Einstein's equations, the four represented by

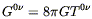
Equation 4.82 (4.82)

cannot be used to evolve the initial data (g$\scriptstyle \mu$$\scriptstyle \nu$,$ \partial_{t}$g$\scriptstyle \mu$$\scriptstyle \nu$)$\scriptstyle \Sigma$. Rather, they serve as constraints on this initial data; we are not free to specify any combination of the metric and its time derivatives on the hypersurface $ \Sigma$, since they must obey the relations (4.82). The remaining equations,

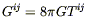
Equation 4.83 (4.83)

are the dynamical evolution equations for the metric. Of course, these are only six equations for the ten unknown functions g$\scriptstyle \mu$$\scriptstyle \nu$(x$\scriptstyle \sigma$), so the solution will inevitably involve a fourfold ambiguity. This is simply the freedom that we have already mentioned, to choose the four coordinate functions throughout spacetime.

It is a straightforward but unenlightening exercise to sift through (4.83) to find that not all second time derivatives of the metric appear. In fact we find that $ \partial_{t}^{2}$gij appears in (4.83), but not $ \partial_{t}^{2}$g0$\scriptstyle \nu$. Therefore a "state" in general relativity will consist of a specification of the spacelike components of the metric gij|$\scriptstyle \Sigma$ and their first time derivatives $ \partial_{t}$gij|$\scriptstyle \Sigma$ on the hypersurface $ \Sigma$, from which we can determine the future evolution using (4.83), up to an unavoidable ambiguity in fixing the remaining components g0$\scriptstyle \nu$. The situation is precisely analogous to that in electromagnetism, where we know that no amount of initial data can suffice to determine the evolution uniquely since there will always be the freedom to perform a gauge transformation A$\scriptstyle \mu$ $ \rightarrow$ A$\scriptstyle \mu$ + $ \partial_{\mu}$$ \lambda$. In general relativity, then, coordinate transformations play a role reminiscent of gauge transformations in electromagnetism, in that they introduce ambiguity into the time evolution.

One way to cope with this problem is to simply "choose a gauge." In electromagnetism this means to place a condition on the vector potential A$\scriptstyle \mu$, which will restrict our freedom to perform gauge transformations. For example we can choose Lorentz gauge, in which $ \nabla_{\mu}^{}$A$\scriptstyle \mu$ = 0, or temporal gauge, in which A0 = 0. We can do a similar thing in general relativity, by fixing our coordinate system. A popular choice is harmonic gauge (also known as Lorentz gauge and a host of other names), in which

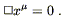
Equation 4.84 (4.84)

Here $ \Box$ = $ \nabla^{\mu}_{}$$ \nabla_{\mu}^{}$ is the covariant D'Alembertian, and it is crucial to realize when we take the covariant derivative that the four functions x$\scriptstyle \mu$ are just functions, not components of a vector. This condition is therefore simply

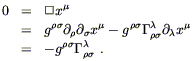
Equation 4.85 (4.85)

In flat space, of course, Cartesian coordinates (in which $ \Gamma^{\lambda}_{\rho\sigma}$ = 0) are harmonic coordinates. (As a general principle, any function f which satisfies $ \Box$f = 0 is called an "harmonic function.")

To see that this choice of coordinates successfully fixes our gauge freedom, let's rewrite the condition (4.84) in a somewhat simpler form. We have

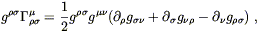
Equation 4.86 (4.86)

from the definition of the Christoffel symbols. Meanwhile, from $ \partial_{\rho}$(g$\scriptstyle \mu$$\scriptstyle \nu$g$\scriptstyle \sigma$$\scriptstyle \nu$) = $ \partial_{\rho}$$ \delta^{\mu}_{\sigma}$ = 0 we have

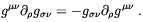
Equation 4.87 (4.87)

Also, from our previous exploration of the variation of the determinant of the metric (4.65), we have

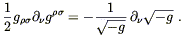
Equation 4.88 (4.88)

Putting it all together, we find that (in general),

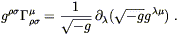
Equation 4.89 (4.89)

The harmonic gauge condition (4.85) therefore is equivalent to

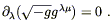
Equation 4.90 (4.90)

Taking the partial derivative of this with respect to t = x0 yields

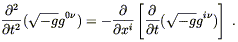
Equation 4.91 (4.91)

This condition represents a second-order differential equation for the previously unconstrained metric components g0$\scriptstyle \nu$, in terms of the given initial data. We have therefore succeeded in fixing our gauge freedom, in that we can now solve for the evolution of the entire metric in harmonic coordinates. (At least locally; we have been glossing over the fact our gauge choice may not be well-defined globally, and we would have to resort to working in patches as usual. The same problem appears in gauge theories in particle physics.) Note that we still have some freedom remaining; our gauge condition (4.84) restricts how the coordinates stretch from our initial hypersurface $ \Sigma$ throughout spacetime, but we can still choose coordinates xi on $ \Sigma$ however we like. This corresponds to the fact that making a coordinate transformation x$\scriptstyle \mu$ $ \rightarrow$ x$\scriptstyle \mu$ + $ \delta^{\mu}_{}$, with $ \Box$$ \delta^{\mu}_{}$ = 0, does not violate the harmonic gauge condition.

We therefore have a well-defined initial value problem for general relativity; a state is specified by the spacelike components of the metric and their time derivatives on a spacelike hypersurface $ \Sigma$; given these, the spacelike components (4.83) of Einstein's equations allow us to evolve the metric forward in time, up to an ambiguity in coordinate choice which may be resolved by choice of gauge. We must keep in mind that the initial data are not arbitrary, but must obey the constraints (4.82). (Once we impose the constraints on some spacelike hypersurface, the equations of motion guarantee that they remain satisfied, as you can check.) The constraints serve a useful purpose, of guaranteeing that the result remains spacetime covariant after we have split our manifold into "space" and "time." Specifically, the Gi0 = 8$ \pi$GTi0 constraint implies that the evolution is independent of our choice of coordinates on $ \Sigma$, while G00 = 8$ \pi$GT00 enforces invariance under different ways of slicing spacetime into spacelike hypersurfaces.

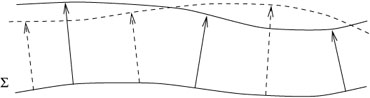
Figure 4.10

Once we have seen how to cast Einstein's equations as an initial value problem, one issue of crucial importance is the existence of solutions to the problem. That is, once we have specified a spacelike hypersurface with initial data, to what extent can we be guaranteed that a unique spacetime will be determined? Although one can do a great deal of hard work to answer this question with some precision, it is fairly simple to get a handle on the ways in which a well-defined solution can fail to exist, which we now consider.

It is simplest to first consider the problem of evolving matter fields on a fixed background spacetime, rather than the evolution of the metric itself. We therefore consider a spacelike hypersurface $ \Sigma$ in some manifold M with fixed metric g$\scriptstyle \mu$$\scriptstyle \nu$, and furthermore look at some connected subset S in $ \Sigma$. Our guiding principle will be that no signals can travel faster than the speed of light; therefore "information" will only flow along timelike or null trajectories (not necessarily geodesics). We define the future domain of dependence of S, denoted D+(S), as the set of all points p such that every past-moving, timelike or null, inextendible curve through p must intersect S. ("Inextendible" just means that the curve goes on forever, not ending at some finite point.) We interpret this definition in such a way that S itself is a subset of D+(S). (Of course a rigorous formulation does not require additional interpretation over and above the definitions, but we are not being as rigorous as we could be right now.) Similarly, we define the past domain of dependence D-(S) in the same way, but with "past-moving" replaced by "future-moving." Generally speaking, some points in M will be in one of the domains of dependence, and some will be outside; we define the boundary of D+(S) to be the future Cauchy horizon H+(S), and likewise the boundary of D-(S) to be the past Cauchy horizon H-(S). You can convince yourself that they are both null surfaces.

Figure 4.11

The usefulness of these definitions should be apparent; if nothing moves faster than light, than signals cannot propagate outside the light cone of any point p. Therefore, if every curve which remains inside this light cone must intersect S, then information specified on S should be sufficient to predict what the situation is at p. (That is, initial data for matter fields given on S can be used to solve for the value of the fields at p.) The set of all points for which we can predict what happens by knowing what happens on S is simply the union D+(S) $ \cup$ D-(S).

We can easily extend these ideas from the subset S to the entire hypersurface $ \Sigma$. The important point is that D+($ \Sigma$) $ \cup$ D-($ \Sigma$) might fail to be all of M, even if $ \Sigma$ itself seems like a perfectly respectable hypersurface that extends throughout space. There are a number of ways in which this can happen. One possibility is that we have just chosen a "bad" hypersurface (although it is hard to give a general prescription for when a hypersurface is bad in this sense). Consider Minkowski space, and a spacelike hypersurface $ \Sigma$ which remains to the past of the light cone of some point.

Figure 4.12

In this case $ \Sigma$ is a nice spacelike surface, but it is clear that D+($ \Sigma$) ends at the light cone, and we cannot use information on $ \Sigma$ to predict what happens throughout Minkowski space. Of course, there are other surfaces we could have picked for which the domain of dependence would have been the entire manifold, so this doesn't worry us too much.

A somewhat more nontrivial example is known as Misner space. This is a two-dimensional spacetime with the topology of $ \bf R^{1}_{}$ × S1, and a metric for which the light cones progressively tilt as you go forward in time.

Figure 4.13

Past a certain point, it is possible to travel on a timelike trajectory which wraps around the S1 and comes back to itself; this is known as a closed timelike curve. If we had specified a surface $ \Sigma$ to this past of this point, then none of the points in the region containing closed timelike curves are in the domain of dependence of $ \Sigma$, since the closed timelike curves themselves do not intersect $ \Sigma$. This is obviously a worse problem than the previous one, since a well-defined initial value problem does not seem to exist in this spacetime. (Actually problems like this are the subject of some current research interest, so I won't claim that the issue is settled.)

A final example is provided by the existence of singularities, points which are not in the manifold even though they can be reached by travelling along a geodesic for a finite distance. Typically these occur when the curvature becomes infinite at some point; if this happens, the point can no longer be said to be part of the spacetime. Such an occurrence can lead to the emergence of a Cauchy horizon - a point p which is in the future of a singularity cannot be in the domain of dependence of a hypersurface to the past of the singularity, because there will be curves from p which simply end at the singularity.

Figure 4.14

All of these obstacles can also arise in the initial value problem for GR, when we try to evolve the metric itself from initial data. However, they are of different degrees of troublesomeness. The possibility of picking a "bad" initial hypersurface does not arise very often, especially since most solutions are found globally (by solving Einstein's equations throughout spacetime). The one situation in which you have to be careful is in numerical solution of Einstein's equations, where a bad choice of hypersurface can lead to numerical difficulties even if in principle a complete solution exists. Closed timelike curves seem to be something that GR works hard to avoid - there are certainly solutions which contain them, but evolution from generic initial data does not usually produce them. Singularities, on the other hand, are practically unavoidable. The simple fact that the gravitational force is always attractive tends to pull matter together, increasing the curvature, and generally leading to some sort of singularity. This is something which we apparently must learn to live with, although there is some hope that a well-defined theory of quantum gravity will eliminate the singularities of classical GR.

Next Contents Previous