


When an isolated point source of ionizing radiation turns on in a neutral medium, the ionized volume initially grows in size at a rate fixed by the emission of UV photons, and an ionization front separating the H II and H I regions propagates into the neutral gas. Most photons travel freely in the ionized bubble, and are absorbed in a transition layer. The evolution of an expanding H II region is governed by the equation
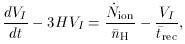
where VI is the proper
volume of the ionized zone, 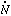 ion is the number of ionizing
photons emitted by the central source per unit time,
ion is the number of ionizing
photons emitted by the central source per unit time, 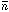 H is the
mean hydrogen density of the expanding IGM, H is the Hubble
constant, and
H is the
mean hydrogen density of the expanding IGM, H is the Hubble
constant, and
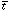 rec is the hydrogen
mean recombination
timescale,
rec is the hydrogen
mean recombination
timescale,
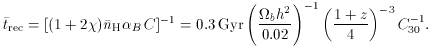
One should point out that the use of a volume-averaged clumping factor,
C  <
nHII2 > /
<
nHII2 > /
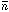 HII2, in the
recombination timescale
is only justified when the size of the H II region is large compared to the
scale of the clumping, so that the effect of many clumps (filaments) within
the ionized volume can be averaged over. The validity of this approximation
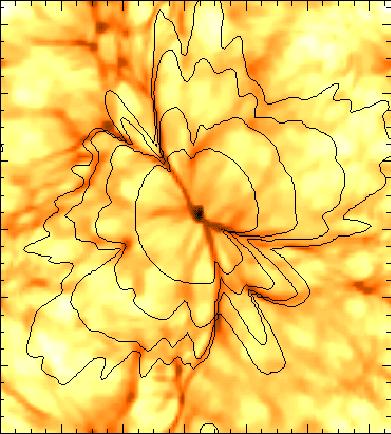
can be tested by numerical simulations (see Figure 7).
Across the I-front the degree of
ionization changes sharply on a distance of the order of the mean free path of
an ionizing photon. When
HII2, in the
recombination timescale
is only justified when the size of the H II region is large compared to the
scale of the clumping, so that the effect of many clumps (filaments) within
the ionized volume can be averaged over. The validity of this approximation
can be tested by numerical simulations (see Figure 7).
Across the I-front the degree of
ionization changes sharply on a distance of the order of the mean free path of
an ionizing photon. When 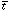 rec is much smaller than the Hubble
time, the growth of the H II region is slowed down by recombinations in
the highly inhomogeneous medium, and its evolution
can be decoupled from the expansion of the universe.
rec is much smaller than the Hubble
time, the growth of the H II region is slowed down by recombinations in
the highly inhomogeneous medium, and its evolution
can be decoupled from the expansion of the universe.
|
Figure 7. Simulating the reionization of
the universe:
propagation of an ionization front in a 1283
cosmological density field. A ``mini-quasar'' with |
In analogy with the individual H II region case, it can be shown that the hydrogen component in a highly inhomogeneous universe is completely reionized when the number of photons emitted above 1 ryd in one recombination time equals the mean number of hydrogen atoms. At any given epoch there is a critical value for the emission rate of ionizing photons per unit cosmological comoving volume,
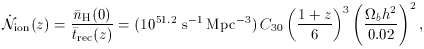
which is independent of the (unknown) previous emission history of
the universe: only
rates above this value will provide enough UV photons to ionize the IGM by
that epoch. One can then compare our estimate of
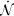 ion to the
inferred contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[20])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 6 (right). While
ion to the
inferred contribution from QSOs and star-forming galaxies.
The uncertainty on this critical rate is difficult to estimate, as it depends
on the clumpiness of the IGM (scaled in the expression above
to the value inferred at z = 5 from numerical simulations
[20])
and the nucleosynthesis constrained baryon density. The
evolution of the critical rate as a function of redshift is plotted in
Figure 6 (right). While
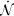 ion is comparable to
the quasar contribution at
z
ion is comparable to
the quasar contribution at
z  3, there is some
indication of a deficit of Lyman-continuum
photons at z = 5. For bright, massive galaxies to produce enough UV
radiation at
z = 5, their space density would have to be comparable to the one
observed at
z
3, there is some
indication of a deficit of Lyman-continuum
photons at z = 5. For bright, massive galaxies to produce enough UV
radiation at
z = 5, their space density would have to be comparable to the one
observed at
z 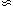 3, with most
ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the
IGM
[31].
(5)
3, with most
ionizing photons being able to escape freely from the
regions of star formation into the IGM. This scenario may be in
conflict with direct observations of local starbursts below
the Lyman limit showing that at most a few percent of the stellar ionizing
radiation produced by these luminous sources actually escapes into the
IGM
[31].
(5)
It is interesting to convert the derived value of
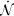 ion
into a ``minimum'' star formation rate per unit (comoving) volume,
ion
into a ``minimum'' star formation rate per unit (comoving) volume,
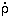 *:
*:
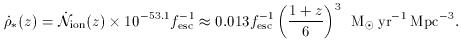
The star formation density given in the equation above is comparable
with the value directly ``observed''
(i.e., uncorrected for dust reddening) at z
 3
[37].
The conversion factor assumes a Salpeter IMF with solar metallicity, and has
been computed using a population synthesis code
[4].
It can be understood by noting that, for each 1 M
3
[37].
The conversion factor assumes a Salpeter IMF with solar metallicity, and has
been computed using a population synthesis code
[4].
It can be understood by noting that, for each 1 M of stars formed,
8% goes into massive stars with M > 20 M
of stars formed,
8% goes into massive stars with M > 20 M that dominate the
Lyman-continuum luminosity of a stellar population. At the end of the C-burning
phase, roughly half of the initial mass is converted into helium and carbon,
with a mass fraction released as radiation of 0.007. About 25% of the energy
radiated away goes
into ionizing photons of mean energy 20 eV. For each 1
M
that dominate the
Lyman-continuum luminosity of a stellar population. At the end of the C-burning
phase, roughly half of the initial mass is converted into helium and carbon,
with a mass fraction released as radiation of 0.007. About 25% of the energy
radiated away goes
into ionizing photons of mean energy 20 eV. For each 1
M of stars
formed every year, we then expect
of stars
formed every year, we then expect
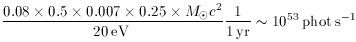
to be emitted shortward of 1 ryd.
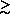 30%.
Back.
30%.
Back.