5.7.2. Multi-field theories
A recent trend in inflationary model building has been the exploration of
models with more than one scalar field. The classic example is the hybrid
inflation model,
[13]
which seems particularly promising for
particle physics model building. The simplest version has a potential
with two fields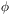 
and
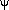of the form
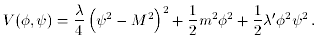
which is illustrated in Figure 4. When
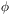2 is large,
the
minimum of the potential in the 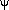-direction
is at 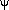= 0. The field rolls down this
`channel' until it reaches
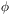inst2 =
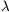M2 /
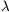', at
which point 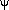= 0 becomes unstable
and the field rolls into one of the
true minima at 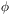= 0 and
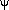= ±M.
|
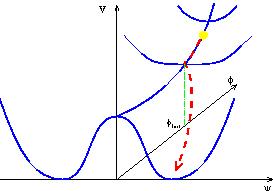
Figure 4. The potential for the hybrid
inflation model. The field rolls down the channel at
|
While in the `channel', which is where all the interesting behaviour takes
place, this is just like a single field model with an effective potential
for 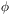of the form
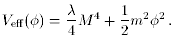
This is a fairly standard form, the unusual thing being the constant term,
which would not normally be allowed as it would give a present-day
cosmological constant. The most interesting regime is where that constant
dominates, and it gives quite an unusual phenomenology. In particular, the
energy density during inflation can be much lower than normal while still
giving suitably large density perturbations, and secondly the field
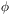can be rolling extremely slowly which is of benefit to particle physics
model building.
Within the more general class of two and multi-field inflation models, it is quite common for only one field to be dynamically important, as in the hybrid inflation model - this effectively reduces the situation back to the single field case of the previous subsection. However, it may also be possible to have more than one important dynamical degree of freedom. In that case there is no attractor behaviour giving a unique route into the potential minimum, as in the single field case; for example, if the potential is of the form of an asymmetric bowl one could roll into the base down any direction. In that situation, the model loses some of its predictive power, because the late-time behaviour is not independent of the initial conditions. (5)
5 Of course, there is no requirement that the `true' physical theory does have predictive power, but it would be unfortunate for us if it does not.