Copyright © 1979 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1979. 17:
135-87 Copyright © 1979 by Annual Reviews. All rights reserved |
The derivation of masses of binary galaxies rests on several important
assumptions. Let us first consider the simplest case of circular
orbits. Assume that the galaxies are gravitationally bound, they
interact as point masses, the distribution of orbital inclinations and
phases is random, there is no intergalactic matter, and there is no
dynamical interaction with matter outside the binary. A full
discussion of this case is given by
Page (1961),
for example, but we
present the rudiments here. Let MT be the mass of each
component (the two masses are assumed equal), R the spatial
separation, and V the
total orbital velocity. Then MT = V2
R / 2G. Owing to projection
effects, V and R are unobservable. One measures instead
 v, the radial
velocity difference, and rp, the projected
separation. These are given
by
v, the radial
velocity difference, and rp, the projected
separation. These are given
by  v = V cos
v = V cos 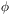 cos
cos 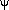 , and rp = R cos
, and rp = R cos 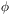 , where
, where 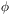 is the angle between
the spatial separation R and the plane of the sky and
is the angle between
the spatial separation R and the plane of the sky and 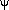 is the angle
between the orbital velocity V and the plane determined by the two
galaxies and the observer. Let us define an ``indicative mass'':
is the angle
between the orbital velocity V and the plane determined by the two
galaxies and the observer. Let us define an ``indicative mass'':
F (MT) is always less than or equal to the true mass
according to the
projection factor cos3
Page (1952)
assumed that for a collection of circular orbits, the
angles
Depending upon the true distribution of spatial separations,
<Fp>
can therefore be a strong function of rp.
Page (1961)
later amended
his treatment to include this dependence. As a model for the spatial
distribution function, he used
an expression empirically derived by
Holmberg (1954).
This distribution produces a marked increase in <Fp> as
rp approaches Rmax,
the maximum spatial separation of binary galaxies. Such a variation in
<Fp>, if real, is quite inconvenient. It means we
cannot compare
indicative mass values F (MT) at different projected
separations without first correcting them for trends in
<Fp>. Comparisons between
independent data sets thus become much more cumbersome.
An important breakthrough in binary galaxy studies has been the
realization that Equation (7) is not correct and that apparently D (R)
is a power law over the observable range 20 to 500 kpc.
Turner (1976a,
b)
and
S. Peterson (1978),
both working from samples of binary
galaxies chosen by means of well-determined selection criteria, find
that D (r)
Fortunately, the sensitivity to
The use of a mean correction factor <Fp> to rectify
the observed
values of F (MT) is unwise for a number of
reasons. First, regardless
of what criteria are employed to select the sample of binaries,
spurious pairs will creep in. Such pairs tend to have large values of
Second, the use of a simple mean ignores all information contained
in the shape of the distribution F (MT) and, more
particularly, in the
bivariate probability density p(
Finally, the distribution of F (MT) is highly skewed,
owing to the
skewness of Fp (
The use of a simple mean projection factor nevertheless provides a
quick and moderately accurate way to compare data sets from various
workers and to estimate the effects of different assumptions
concerning the geometry of the orbits. From the work of
Turner (1976b),
who analyzed his data using both a simple mean and a more
elaborate technique (see below), we estimate that use of the simple
mean yields results accurate to ±20%.
Because of the greater complexity of analyzing noncircular orbits,
the general solution analogous to Equation (8) has not yet been
derived. If the orbits are eccentric, the angles
The success of the binary method clearly depends on being able to
identify pairs that are real physical systems. The first discussion of
this problem and the resulting catalog of doubles was prepared by
Holmberg (1937).
Other major lists having historical interest include
Vorontsov-Velyaminov's Atlas of Interacting Galaxies
(1959), Arp's
Atlas of Peculiar
Galaxies (1966),
and Karachentsev's comprehensive list of 603 pairs
(Karachentsev 1972).
Recent velocity measurements have been published by
Karachentsev et
al. (1976),
Karachentsev (1978),
Turner (1976a), and
S. Peterson (1978).
In all, there have been four major studies of masses in binary
galaxies. Page's work
(Page 1961,
1962)
was the standard reference for
many years. Assuming Holmberg's relation (Equation 7) and circular
orbits, he obtained M / LB = 0.7±0.9 for
spiral-spiral pairs and M / LB =
46±46 for pairs containing ellipticals and/or S0's (corrected to
H0 = 50 km sec-1 Mpc-1). The
value for spirals is much smaller than the
average of ~ 5 within the Holmberg radius derived in
Section 2, while
the value for early-type galaxies is significantly larger than our
estimates for single galaxies presented in
Section 3.
Turner (1976a,
b)
introduced a new standard of rigor into the study
of binary galaxies by selecting a binary sample according to
well-defined criteria and using, instead of the traditional mean
projection correction <
S. Peterson (1978)
applied a rank-sum procedure to the distribution
F (MT). His analysis was confined to the case of
circular orbits, but
his radial velocities, many of which came from 21-cm measurements,
were more accurate than Turner's largely optical velocities. His
selection criteria also differed from Turner's: his binaries were less
isolated but extended to much larger radial separations because no
outer angular cutoff was employed.
In Table 4 Turner's and Peterson's
results for spiral-spiral pairs
are compared. The original values of M / LB given by
these authors have
been corrected to our system. For reference,
Table 4 also includes
median values of
Inspection of Table 4 shows that
values of M / LB derived by various
authors differ substantially. Is this discrepancy due to differences
in the data sets or to differences in statistical treatment? To answer
this question, it is helpful to consider just those values based on
the assumption of point masses, circular orbits, and
Histograms of
On the other hand, the three samples differ markedly in their
distribution of projected separation, rp. Evidently
Karachentsev's
sample primarily includes rather close pairs, a conclusion supported
by the high percentage of interacting galaxies in his sample
(Karachentsev 1977).
Turner's sample is intermediate, while
Peterson's, chosen without any arbitrary cutoff in angular separation,
contains many very wide binaries.
It seems to us that these results are consistent with an increase in
M / LB with radius, as would be expected from massive
envelopes. This
view is supported by the fact that M / LB for
Peterson's outermost pairs
(with rp > 112 kpc) is in good agreement with M /
LB for Turner's sample
if massive halos having radii of 100 kpc are assumed. Peterson
furthermore finds that MT increases linearly with
rp out to ~ 100 kpc
and then levels off, whereas
In our opinion the data are not yet strong enough to take any of
these radial trends too seriously, and the global result must be given
highest weight. Taken as a whole, the binary data of Turner and
Peterson imply that M / LB
Before continuing, it is of interest to inquire why Page with
essentially similar data obtained a much lower value of M /
LB for
spiral-spiral pairs. According to Peterson, the difference is due to
Page's weighting scheme, which set weights inversely proportional to
the square of the variance in (
The high M / LB values determined from binary galaxies
are subject to
several potential sources of uncertainty. The first arises from
observational errors in the velocity differences. Let us suppose that
there were no actual increase in M / LB beyond
RHO. Then velocities
would decline approximately as r-1/2, and at a
distance of 100 kpc, we would predict orbital velocity differences of
roughly 140 km s-1. The
observed velocity difference
Although simple, this argument approaches the problem in backwards
fashion. The proper question is whether the full width of the observed
histogram of
The second problem which might affect the results is contamination
by spurious pairs. Turner was able to show conclusively that his
sample is not appreciably contaminated by objects in the distant
foreground or background. However, a great many of Turner's and
Peterson's binaries are members of small groups of galaxies, in which
the problem of contamination by foreground and background group
members could be serious. Statistical estimates of the frequency of
spurious pairs made to date are unsatisfactory because they do not
include a probable spatial correlation between the target galaxy and
contaminating galaxies. Furthermore, the relative velocities of group
members, typically a few hundred km s-1, are just in the range where
much of the information in the
Yahil (1977)
has pointed out a disturbing fact which may be related
to contamination problems. He has searched for a positive correlation
between F (MT) and the combined luminosity of
the pair. Even though
variations in <
To investigate the contamination problem further, it would be
extremely useful to compile a binary sample having significantly more
stringent isolation criteria than those used heretofore. At the very
least, one might test whether M / LB is noticeably
smaller for those
binaries in existing samples having only distant neighbors but
sizeable spatial separations. Note that an analysis confined to just
those binaries that show obvious Signs of interaction will not help to
test the existence of dark material, since such pairs have separations
not much larger than the Holmberg radius. They therefore should have
rather small M / LB.
For the moment we continue to assume that the masses for
spiral-spiral pairs as measured by binary galaxies are real, but the
exact value of the mass-to-light ratio remains somewhat doubtful until
the problem of contamination is conclusively cleared up.
Turning now to binary mass determinations for early-type galaxies,
we recall Page's finding that E and S0 galaxies have much larger M /
LB
than spirals. Both Turner and Peterson obtained a similar result,
although their measured differences are smaller: Turner finds the
ratio to be 2.0±0.5, while Peterson obtains 1.7 with larger errors.
Actually it seems more probable that most of the mixed E-spiral
pairs identified to date are not in fact physically bound to one
another. The evidence for this assertion can be found in
Figure 4,
which presents distributions of
This disparity between E's and spirals was first noticed by K.C.
Freeman and T.S. Van Albada (in preparation) for Turner's pairs. The
existence of the same trend in Peterson's data, which is an
essentially independent sample, is strong confirmation that the effect
is real. We conclude that few if any of the pairs containing
elliptical galaxies are physical associations. Virtually all the E
pairs are members of groups or clusters, and it seems likely that they
are due to chance superpositions of cluster members.
The great majority of these E pairs are mixed, that is, only one
member is an E galaxy. Very few are EE pairs, and their small number
does not allow us to test whether they, in contrast to the mixed
pairs, are physically associated. One conclusion seems probable,
however. Although luminous ellipticals and spirals are quite commonly
associated with one another in groups, close associations in binaries
are rare. This fact might be an important clue to processes which
determine the Hubble type.
Histograms for S0 pairs are shown for comparison in
Figure 4 as the
hatched areas. The S0 distributions apparently resemble those of
spirals more closely, so that S0-spiral binaries probably exist. It is
this fact which is responsible for the queer nature of the E pairs
having escaped discovery before now: since E and S0 pairs have
traditionally been lumped together, the peculiar histogram of the
ellipticals was diluted by the more normal one for the S0's.
If these mixed E pairs are indeed not physical associations, there
exists at present virtually no reliable information on masses of
early-type galaxies in binary systems.
Jenner (1974)
studied the
motions of the companions of cD galaxies, but only ten pairs were
included. Using his mean mass to obtain M / LB on our
system, we find
M / LB ~ 50 at 60 kpc spatial separation. However, if
one system with
extremely large
We found in Section 3 that data on M /
L for S0 galaxies within RHO
are scanty, while those for ellipticals are nonexistent. The binary
data are likewise fragmentary for these early morphological types. The
results of Jenner and Smart, however, suggest that the mass-to-light
ratio of E and S0 galaxies are broadly similar to those of later-type spirals.
Although the binary data seem to imply the existence of dark matter,
we encounter a possible problem when trying to estimate the extent of
the dark envelopes from these data. Such an estimate can be made in
two ways. First, we have the results of Turner's model simulations,
which ruled out envelopes larger than 100 kpc in extent. Second, we
have the estimates of global M / LB from Turner's halo
model and also
from Peterson's widely-spaced pairs. These both yield M /
LB
These estimates are in fair agreement with one another, but are
marginally at variance with the conclusions of
White & Sharp (1977),
who pointed out that spherical halos around close binaries must
interpenetrate strongly and that the effects of dynamical friction
will be severe. In fact, two binaries ought to merge completely within
an orbital period if their distance of closest approach is less than
three times the half-mass radii (r1/2) of the
halos. For Turner's sample, this implies that the mean value of
r1/2 is less than 58 kpc,
and hence that r, the outer boundary of the halo, is less than 116 kpc
for the usual halo model. This limit must be reduced even further if
the orbits are appreciably eccentric.
Even though this limit is barely consistent with Turner's estimate,
many individual binaries must have true spatial separations much
smaller than 100 kpc, and their envelopes should interpenetrate
strongly. How are they then able to persist? Perhaps the outer
envelope radius varies widely from galaxy to galaxy. Close pairs might
then simply be those objects with initially small envelopes the others
having already merged long ago. This reasoning would suggest that the
observed radial distribution function for binaries, D (R), is strongly
determined by the initial distribution function for the envelope radii
themselves and that the binaries we see today are just those which
were able to survive over a long period of time. In this regard, we
recall the suggestion that merged galaxies become ellipticals
(Toomre 1977,
White 1978);
this effect might then explain the rarity of E binaries.
As White and Sharp point out, the dynamics of binary galaxies, if
analyzed from this more general point of view, might well place severe
constraints on the distribution of unseen matter. N. Krumm (private
communication) has emphasized the advantages of studying interacting
pairs because of the information they afford in disentangling
projection effects, which make the study of ordinary binaries so
difficult. Tidal tails in interacting galaxies might have
significantly different shapes if the gravitational effect of dark
envelopes were included. In short, dynamical modelling of binary
galaxies including the effects of halos seems a fruitful area for
observer and theorist alike in the near future.
In summary, for spatial separations greater than 100 kpc, the binary
data indicate M / LB 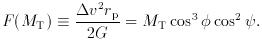
 cos
cos 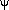
 Fp (
Fp (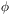 ,
, 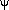 ). To obtain the true mass in
the simplest possible way, we can average over some appropriate
statistical sample to derive a mean projection factor. Then, in
principle, for a large enough statistical sample,
). To obtain the true mass in
the simplest possible way, we can average over some appropriate
statistical sample to derive a mean projection factor. Then, in
principle, for a large enough statistical sample,
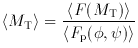
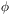 and
and 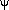 are randomly oriented, whence
<Fp> = 3
are randomly oriented, whence
<Fp> = 3 / 32 =
0.295. This assumption is unrealistic because binary galaxies are
selected and analyzed on the basis of their projected separation,
rp. Once rp is specified,
/ 32 =
0.295. This assumption is unrealistic because binary galaxies are
selected and analyzed on the basis of their projected separation,
rp. Once rp is specified, 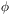 is no longer a random variable. The
distribution of true spatial separations combines with the observed
rp to make certain values of
is no longer a random variable. The
distribution of true spatial separations combines with the observed
rp to make certain values of 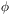 more likely than others.
more likely than others.
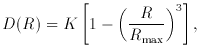
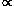 R-
R-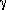 where
where 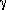 = 0.5±0.1. Since
a power law has no
scale-length, <Fp> is independent of
rp and is given by (Peterson 1978):
= 0.5±0.1. Since
a power law has no
scale-length, <Fp> is independent of
rp and is given by (Peterson 1978):
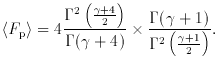
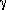 is not great; over the range
is not great; over the range 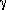 = 0.0
to
= 0.0
to 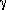 = 1.0,
<Fp> increases from 0.212 to 0.295. The fact that the
projection factor is independent of radius for a power law makes the
analysis much more transparent since radial trends in mass and M /
LB
can now be determined immediately from trends in indicative mass.
= 1.0,
<Fp> increases from 0.212 to 0.295. The fact that the
projection factor is independent of radius for a power law makes the
analysis much more transparent since radial trends in mass and M /
LB
can now be determined immediately from trends in indicative mass.
 v2 and hence
of F (MT). Thus <MT> for the sample
is sensitive to the
adopted cutoff in
v2 and hence
of F (MT). Thus <MT> for the sample
is sensitive to the
adopted cutoff in  v. To
avoid this difficulty, one should use a
method based on the entire distribution F (MT) and
which weights the observations more or less equally.
v. To
avoid this difficulty, one should use a
method based on the entire distribution F (MT) and
which weights the observations more or less equally.
 v, rp). As pointed out by
Noerdlinger (1975),
p(
v, rp). As pointed out by
Noerdlinger (1975),
p( v, rp) is sensitive to the orbital
eccentricities of galaxies
in the sample.
Turner (1976b)
was able to rule out rather conclusively
highly eccentric models for binary orbits on this basis.
v, rp) is sensitive to the orbital
eccentricities of galaxies
in the sample.
Turner (1976b)
was able to rule out rather conclusively
highly eccentric models for binary orbits on this basis.
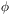 ,
,
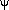 ) itself. F (MT)
peaks strongly at zero, and for
circular orbits the median value of F (MT) is only 11%
of the value of
<MT> ultimately derived. Peterson argues that such a skewed
distribution is not well represented by its mean.
) itself. F (MT)
peaks strongly at zero, and for
circular orbits the median value of F (MT) is only 11%
of the value of
<MT> ultimately derived. Peterson argues that such a skewed
distribution is not well represented by its mean.
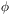 and
and 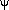 as defined in
this section are not applicable. Nevertheless, a mean projection
factor still exists, call it <
as defined in
this section are not applicable. Nevertheless, a mean projection
factor still exists, call it <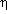 >, which reduces to <Fp> in the
circular case.
Karachentsev (1970) and
Noerdlinger (1975) have
calculated values of <
>, which reduces to <Fp> in the
circular case.
Karachentsev (1970) and
Noerdlinger (1975) have
calculated values of <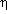 > for collections of binaries with eccentric
orbits. However, in their existing form these expressions share the
same drawback as Page's original estimate: they do not take into
account the bias introduced into the angle
> for collections of binaries with eccentric
orbits. However, in their existing form these expressions share the
same drawback as Page's original estimate: they do not take into
account the bias introduced into the angle 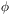 once rp is specified. To
treat the noncircular case, it would seem best at present to rely on
Turner's model simulations of binaries with various
eccentricities. These show that, for eccentric orbits, the projection
factor is smaller and the derived masses therefore larger. If
once rp is specified. To
treat the noncircular case, it would seem best at present to rely on
Turner's model simulations of binaries with various
eccentricities. These show that, for eccentric orbits, the projection
factor is smaller and the derived masses therefore larger. If 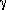 = 0.5,
for example, the minimum value of <
= 0.5,
for example, the minimum value of <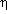 > is 0.105 for purely radial
orbits, compared to 0.261 for circular orbits. Qualitatively this
effect is easy to understand: if the orbits are eccentric, one views
them preferentially near apogalacticon, where the kinetic energies are
lower than average. Therefore the observed F (MT) are
systematically lower than in the circular case.
> is 0.105 for purely radial
orbits, compared to 0.261 for circular orbits. Qualitatively this
effect is easy to understand: if the orbits are eccentric, one views
them preferentially near apogalacticon, where the kinetic energies are
lower than average. Therefore the observed F (MT) are
systematically lower than in the circular case.
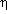 >, a rank-sum test that essentially compared
the observed frequency distribution p (
>, a rank-sum test that essentially compared
the observed frequency distribution p ( v, rp) with simulated versions of
p (
v, rp) with simulated versions of
p ( v,
rp) for various orbital eccentricities. He was also
able to model
extended spherical halos surrounding the galaxies. Using the shape of
the distribution p (
v,
rp) for various orbital eccentricities. He was also
able to model
extended spherical halos surrounding the galaxies. Using the shape of
the distribution p ( v, rp), he showed that binary
orbits cannot be
highly eccentric and that if massive halos are present, they must have
radii
v, rp), he showed that binary
orbits cannot be
highly eccentric and that if massive halos are present, they must have
radii 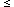 100 kpc.
100 kpc.
 v and
rp for the Turner and Peterson samples. We
have also reduced the results of Karachenstev
(1977,
1978)
to our system and included them in
Table 4. Unfortunately only fragmentary
accounts of Karachentsev's work were available to us, and we have had
to combine results from several different papers. Details appear in
the footnotes. We regret any inaccuracies introduced by this procedure.
v and
rp for the Turner and Peterson samples. We
have also reduced the results of Karachenstev
(1977,
1978)
to our system and included them in
Table 4. Unfortunately only fragmentary
accounts of Karachentsev's work were available to us, and we have had
to combine results from several different papers. Details appear in
the footnotes. We regret any inaccuracies introduced by this procedure.
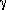 = 0.5. (We have
provided an additional entry for Karachentsev's data which converts
his results to this case.) We then obtain M / LB
(Turner) = 17±4, M / LB
(Peterson) = 32±11, and M / LB (Karachentsev) =
5.9±2.7, values which
still differ by more than the observational errors. Therefore the
differences must be due to the data themselves.
= 0.5. (We have
provided an additional entry for Karachentsev's data which converts
his results to this case.) We then obtain M / LB
(Turner) = 17±4, M / LB
(Peterson) = 32±11, and M / LB (Karachentsev) =
5.9±2.7, values which
still differ by more than the observational errors. Therefore the
differences must be due to the data themselves.

 v
(uncorrected for observational errors) for all
three samples are quite similar. The median values of
v
(uncorrected for observational errors) for all
three samples are quite similar. The median values of  v (for
v (for  v
v 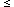 750
km sec-1) in Table 4 confirm this
fact. Thus, the observed
differences in the
750
km sec-1) in Table 4 confirm this
fact. Thus, the observed
differences in the  v
distributions do not seem large enough to
account for the discrepancy in M / LB (see below).
v
distributions do not seem large enough to
account for the discrepancy in M / LB (see below).
 v is constant out to ~ 100 kpc, and then
begins to decline. Although of limited statistical significance
(Peterson's radial bins overlap), this behavior is also consistent
with the existence of massive envelopes having a limited extent. On
the other hand, the same data also show that although
MT increases
with rp out to 100 kpc, M / LB
appears to be approximately constant from
20 kpc to 500 kpc, a result which Peterson takes as strong evidence
against massive envelopes.
v is constant out to ~ 100 kpc, and then
begins to decline. Although of limited statistical significance
(Peterson's radial bins overlap), this behavior is also consistent
with the existence of massive envelopes having a limited extent. On
the other hand, the same data also show that although
MT increases
with rp out to 100 kpc, M / LB
appears to be approximately constant from
20 kpc to 500 kpc, a result which Peterson takes as strong evidence
against massive envelopes.
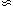 35 at large separations. As the average
value for spirals within the Holmberg radius is only ~ 5, this result
would seem to argue convincingly for additional mass beyond
RHO.
35 at large separations. As the average
value for spirals within the Holmberg radius is only ~ 5, this result
would seem to argue convincingly for additional mass beyond
RHO.
 v)2 due to observational error. Small
observed values of
v)2 due to observational error. Small
observed values of  v therefore are given very high weight, which acts
to reduce the calculated MT and hence M /
LB. Page's method also gives
highest weight to pairs with small separations (large
1/rp). If M / LB
does increase with radius, this effect would further shift M /
LB to
systematically smaller values. Both Turner and Peterson have subjected
their data to Page's scheme of analysis and confirm the fact that the
method yields spuriously low values.
v therefore are given very high weight, which acts
to reduce the calculated MT and hence M /
LB. Page's method also gives
highest weight to pairs with small separations (large
1/rp). If M / LB
does increase with radius, this effect would further shift M /
LB to
systematically smaller values. Both Turner and Peterson have subjected
their data to Page's scheme of analysis and confirm the fact that the
method yields spuriously low values.
 v is further reduced by the projection
factor cos
v is further reduced by the projection
factor cos 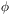 cos
cos 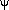 , the mean value of which is roughly 0.46 (for
circular orbits). The expected
, the mean value of which is roughly 0.46 (for
circular orbits). The expected  v on this hypothesis is therefore
only ~ 65 km s-1. Since this is comparable to the precision
of typical optical velocities, it has therefore been argued that existing data
are biased against low mass-to-light ratios.
v on this hypothesis is therefore
only ~ 65 km s-1. Since this is comparable to the precision
of typical optical velocities, it has therefore been argued that existing data
are biased against low mass-to-light ratios.
 v's is
essentially all due to observational error, for
only if this is the case can we substantially reduce the measured
values of M / LB. Peterson's 21-cm velocities are most
useful in
answering this question because of their high accuracy, typically
better than ±20 km s-1. M / LB for
this subsample (30 pairs) is actually
slightly larger than for his sample as a whole. Furthermore, the
v's is
essentially all due to observational error, for
only if this is the case can we substantially reduce the measured
values of M / LB. Peterson's 21-cm velocities are most
useful in
answering this question because of their high accuracy, typically
better than ±20 km s-1. M / LB for
this subsample (30 pairs) is actually
slightly larger than for his sample as a whole. Furthermore, the  v
distribution for pairs with 21-cm velocities is very similar to that
for pairs having at least one optical velocity. Both these tests
indicate that the optical velocities are substantially
correct. L. Schweizer (in preparation) and
Karachentsev (1978)
are currently collecting new, highly accurate velocities for binary
galaxies which should fully resolve this question. For the moment,
however, we are inclined to believe that the velocities are not at fault.
v
distribution for pairs with 21-cm velocities is very similar to that
for pairs having at least one optical velocity. Both these tests
indicate that the optical velocities are substantially
correct. L. Schweizer (in preparation) and
Karachentsev (1978)
are currently collecting new, highly accurate velocities for binary
galaxies which should fully resolve this question. For the moment,
however, we are inclined to believe that the velocities are not at fault.
 v distribution resides.
v distribution resides.
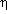 >
produce a large spread in F (MT), Yahil predicts that
there should be a marked correlation between F (MT)
and luminosity, provided binaries have uniform M /
LB. For Turner's sample, no
correlation is found, indicating that M / LB must vary
over at least one
order of magnitude. The correlations between F (MT)
and luminosity for
the Peterson and Karachentsev samples appear similar, supporting this
conclusion. To Yahil, this result suggests that the large-scale
distribution of matter in the universe is not strongly coupled to the
distribution of luminous matter, and that the concept of mass-to-light
ratio is not useful on scales much larger than 10 kpc. Alternatively,
one might conclude that the lack of correlation is caused by errors in
F (MT) introduced by the inclusion of spurious
pairs. Yet the observed
distribution of radial separations, D (R), suggests that the majority
of pairs must be real. If they were chance alignments, D (R) would
increase roughly as R for small separations, whereas the observed
distribution is peaked near zero, suggesting real physical association.
>
produce a large spread in F (MT), Yahil predicts that
there should be a marked correlation between F (MT)
and luminosity, provided binaries have uniform M /
LB. For Turner's sample, no
correlation is found, indicating that M / LB must vary
over at least one
order of magnitude. The correlations between F (MT)
and luminosity for
the Peterson and Karachentsev samples appear similar, supporting this
conclusion. To Yahil, this result suggests that the large-scale
distribution of matter in the universe is not strongly coupled to the
distribution of luminous matter, and that the concept of mass-to-light
ratio is not useful on scales much larger than 10 kpc. Alternatively,
one might conclude that the lack of correlation is caused by errors in
F (MT) introduced by the inclusion of spurious
pairs. Yet the observed
distribution of radial separations, D (R), suggests that the majority
of pairs must be real. If they were chance alignments, D (R) would
increase roughly as R for small separations, whereas the observed
distribution is peaked near zero, suggesting real physical association.
 v for Turner and Peterson's data. For
simplicity let us assume circular orbits, although our conclusion does
not rest on this assumption. For a sample of binary galaxies that are
real physical pairs, we expect that the distribution of
v for Turner and Peterson's data. For
simplicity let us assume circular orbits, although our conclusion does
not rest on this assumption. For a sample of binary galaxies that are
real physical pairs, we expect that the distribution of  v's will
always be peaked at zero owing to the effect of the projection factor
cos
v's will
always be peaked at zero owing to the effect of the projection factor
cos 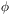 cos
cos 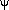 . This prediction is verified for spiral-spiral pairs
(lower histograms). But the upper distributions, in which at least one
member is an E galaxy, are nearly flat, with little or no peak at
zero. The Kolmogorov-Smirnov test
(Hollander & Wolfe
1973)
shows quantitatively that the E and spiral distributions are unlikely to be
drawn from the same population. The probability for the Turner sample
is only 8% and that for the Peterson sample is only 3%. This test
therefore confirms the fact that the samples really are quite different.
. This prediction is verified for spiral-spiral pairs
(lower histograms). But the upper distributions, in which at least one
member is an E galaxy, are nearly flat, with little or no peak at
zero. The Kolmogorov-Smirnov test
(Hollander & Wolfe
1973)
shows quantitatively that the E and spiral distributions are unlikely to be
drawn from the same population. The probability for the Turner sample
is only 8% and that for the Peterson sample is only 3%. This test
therefore confirms the fact that the samples really are quite different.
 v is
omitted, M / LB drops to only ~ 15.
Smart (1973)
obtained results consistent with Jenner's.
v is
omitted, M / LB drops to only ~ 15.
Smart (1973)
obtained results consistent with Jenner's.
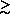 35 at
large separations (the value is a lower limit because both estimates
assume circular orbits). According to the usual version of the massive
halo hypothesis, M / LB (R)
35 at
large separations (the value is a lower limit because both estimates
assume circular orbits). According to the usual version of the massive
halo hypothesis, M / LB (R) 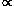 R. Since the average value of M /
LB within
RHO is ~ 5 for spirals, the extent of the envelopes
must be greater than or equal to ~ 7 RHO, or
R. Since the average value of M /
LB within
RHO is ~ 5 for spirals, the extent of the envelopes
must be greater than or equal to ~ 7 RHO, or 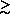 150 kpc.
150 kpc.
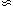 35-50, where the higher value applies if the
orbits have moderate eccentricity (
35-50, where the higher value applies if the
orbits have moderate eccentricity (
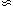 0.7).
0.7).