


3.2.2. Clusters of Galaxies
These are prominent structures which are easily identified on large scale photographic plates. The best studied nearby rich cluster is the Coma cluster of Galaxies shown in Figure 3-3. Clusters of galaxies are subjectively classified according to a "richness" criteria. This criteria is basically the number of "bright" galaxies that appear within a fixed angular radius on the Palomar or ESO Sky Survey plates. A typical cluster detected in this manner has 100-1000 "bright" galaxies. Based on this somewhat loose criterion, George Abell and collaborators have cataloged approximately 4500 clusters of galaxies (see Abell et al. 1989). While some of these cataloged clusters are not real but instead accidental projections of groups along the line of sight, most are gravitationally bound units. These clusters of galaxies generally have three components, although only two of them are accounted for in the typical fit of the cluster density profile:

| (6) |
where  (0) is the central
surface density of galaxies, r0 is the core radius and
(0) is the central
surface density of galaxies, r0 is the core radius and
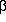 is the slope of
the power law
that characterizes the radial fall off in surface density,
is the slope of
the power law
that characterizes the radial fall off in surface density,
 r.
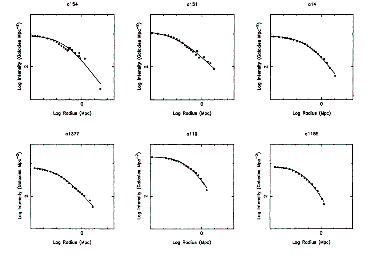
Figure 3-4 shows a selection of surface
density profiles for clusters. The three structural components of clusters are:
r.
Figure 3-4 shows a selection of surface
density profiles for clusters. The three structural components of clusters are:

|
Figure 3-3: CCD image of the center of the Coma Cluster, the richest nearby cluster. The center is dominated by many elliptical and SO galaxies. |
|
Figure 3-4: A sample of cluster density profiles showing the variations in the outer fall off. Data come from West and Bothun (1990). |
1. A core (r0) - this is a region where the projected
surface density
of galaxies is relatively flat. Not all clusters exhibit this feature.
For those that do, the central densities can be quite high.
These densities can be estimated
by measuring  (0),
r0 and the central velocity dispersion.
For an isothermal sphere, the relation between r0 and
(0),
r0 and the central velocity dispersion.
For an isothermal sphere, the relation between r0 and
 0 is:
0 is:

|
In the case of Coma the core radius is
 300 kpc and the central
density is
300 kpc and the central
density is  0.008
M
0.008
M pc-3. This central density is
105 - 106 times higher than the average density of
the Universe. In this
high density region, spiral galaxies are almost never found.
pc-3. This central density is
105 - 106 times higher than the average density of
the Universe. In this
high density region, spiral galaxies are almost never found.
2. The  region -
this is where the surface density profile
begins to fall off. In practice, one can define the "cluster"
as the radius which encloses a density contrast of 100. This radius
depends upon the slope
region -
this is where the surface density profile
begins to fall off. In practice, one can define the "cluster"
as the radius which encloses a density contrast of 100. This radius
depends upon the slope
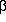 in equation
6. Clusters of galaxies
show large variations in this slope. Some have very extended
regions that contain many galaxies while others have sufficiently
step profiles that most of the galaxies are contained in the
r0
region. If the cluster contains any spiral galaxies they will most
likely be found outside of this region.
in equation
6. Clusters of galaxies
show large variations in this slope. Some have very extended
regions that contain many galaxies while others have sufficiently
step profiles that most of the galaxies are contained in the
r0
region. If the cluster contains any spiral galaxies they will most
likely be found outside of this region.
3. The infalling region - while not normally viewed as a structural
component to clusters, we discuss it here because
delayed infall from this region will augment both the
r0 and 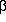 regions over a Hubble time. Most of the infalling galaxies will
be spirals. This infall causes slow evolution of
the density profile as cluster relaxation times are long (see below).
Without accurate distances, however, it is impossible to determine
which galaxies are in the
regions over a Hubble time. Most of the infalling galaxies will
be spirals. This infall causes slow evolution of
the density profile as cluster relaxation times are long (see below).
Without accurate distances, however, it is impossible to determine
which galaxies are in the
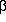 region and which
are still infalling.
region and which
are still infalling.
Evidence that Clusters of Galaxies are Gravitationally Bound
Evidence that clusters of galaxies are gravitationally bound comes in a variety of forms:
1. The galaxy density is quite high and leads to values of over density in the range 100-1000. This range of overdensity is sufficient for the velocities of member galaxies to become virialized. The typical 3D velocity dispersion is 1500 km s-1 whereas the expansion velocity over the scale of the cluster is 100-200 km s-1.
2. Most clusters are sources of intense X-ray emission with typical temperatures of 2-10 Kev. Such high temperatures are best obtained as a result of gas in hydrostatic equilibrium with respect to a deep gravitational potential. This X-ray emission is also well bounded and usually has a density profile that falls off in a manner similar to, or slightly shallower than, the galaxy surface density profile (although we note that cluster X-ray profiles are somewhat hard to measure due to low S/N in the X-ray data).
3. Deep CCD surveys of the sky have shown the existence of clusters of
galaxies at z  1 that look
very much like the present-day
core of the Coma cluster (see
Castander et al. 1994; Postman et al. 1996).
This indicates that a) some rich cluster cores did form early-on and b) in
these rich clusters there has been little evolution of the core
population over the last few
billion years. This is not to say that augmentation of cluster cores
by delayed infall is not occurring, but rather that, out to z = 1 you
can find examples of cluster cores which are as dense as that seen
in Coma.
1 that look
very much like the present-day
core of the Coma cluster (see
Castander et al. 1994; Postman et al. 1996).
This indicates that a) some rich cluster cores did form early-on and b) in
these rich clusters there has been little evolution of the core
population over the last few
billion years. This is not to say that augmentation of cluster cores
by delayed infall is not occurring, but rather that, out to z = 1 you
can find examples of cluster cores which are as dense as that seen
in Coma.
Cluster Timescales
There are several relevant timescales associated with clusters of galaxies and they include the following
 Dynamical Time Scale: This
can be thought of as the time
it takes for the cluster to communicate with itself through its
own potential. There are many different ways to estimate this time
scale but they all scale has
Dynamical Time Scale: This
can be thought of as the time
it takes for the cluster to communicate with itself through its
own potential. There are many different ways to estimate this time
scale but they all scale has
 clust-1/2, which is essentially
the gravitational free-fall time. The most convenient way to define
the dynamical timescale is in terms of the crossing-time. This
crossing time is
clust-1/2, which is essentially
the gravitational free-fall time. The most convenient way to define
the dynamical timescale is in terms of the crossing-time. This
crossing time is

| (7) |
where Rcl is the characteristic cluster radius and V3 is the three dimensional velocity dispersion. For any system of mass particles influenced by small larger scale potential, application of the Virial Theorem can be done after 1 dynamical timescale has elapsed. This allows the systems mass to be estimated from Rcl and V3 as

| (8) |
For a spherical system

| (9) |
Substituting this into equation 8 yields

| (10) |
meaning that R / V 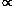
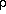 clust-1/2.
This result can also be arrived by considering the time it would take
for a sound wave to cross the cluster or the timescale of gravitational
free fall collapse. Equation 11 below is a convenient parameterization
of the dynamical timescale in terms of observables:
clust-1/2.
This result can also be arrived by considering the time it would take
for a sound wave to cross the cluster or the timescale of gravitational
free fall collapse. Equation 11 below is a convenient parameterization
of the dynamical timescale in terms of observables:
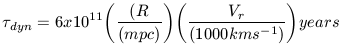
| (11) |
where Vr is the radial component of the three-dimensional
velocity dispersion. A typical cluster has R = 1 and
Vr = 1000 km s-1
which leads to  dyn ~
109 years or roughly 10% of the expansion age.
dyn ~
109 years or roughly 10% of the expansion age.
 Relaxation Timescale: The
relaxation timescale is the
characteristic timescale over which equipartition of energy among
all the particles in the potential occurs.
In such a situation mass segregation occurs with the lighter
galaxies having larger v than the heavier galaxies as all galaxies
have the same value of 1 / 2mv2. As the mass range
for "bright" cluster galaxies is
Relaxation Timescale: The
relaxation timescale is the
characteristic timescale over which equipartition of energy among
all the particles in the potential occurs.
In such a situation mass segregation occurs with the lighter
galaxies having larger v than the heavier galaxies as all galaxies
have the same value of 1 / 2mv2. As the mass range
for "bright" cluster galaxies is  100, the corresponding range
in v would be 10. Thus mass segregation should be relatively easy
to verify as a cluster of galaxies would exhibit their brightest galaxies
in the cluster core and the fainter galaxies preferentially on the outside.
Relaxation can also dynamically heat the very lightest galaxies to
escape velocity.
To date there has been no convincing evidence that mass segregation
in any cluster has occurred. While some clusters
(see below) are dominated by a central massive galaxy which continues
to grow as a result of the assimilation (cannibalism) of other
cluster members, this is not a relaxation effect. The lack of
observed mass segregation helps constrain the overall ages of
clusters of galaxies.
100, the corresponding range
in v would be 10. Thus mass segregation should be relatively easy
to verify as a cluster of galaxies would exhibit their brightest galaxies
in the cluster core and the fainter galaxies preferentially on the outside.
Relaxation can also dynamically heat the very lightest galaxies to
escape velocity.
To date there has been no convincing evidence that mass segregation
in any cluster has occurred. While some clusters
(see below) are dominated by a central massive galaxy which continues
to grow as a result of the assimilation (cannibalism) of other
cluster members, this is not a relaxation effect. The lack of
observed mass segregation helps constrain the overall ages of
clusters of galaxies.
Relaxation is motivated by two kinds of interactions: short range two-body encounters between the individual cluster members and long-range forces due to the smooth cluster potential. In a gravitating system of N-bodies there are two reasonable physical limits that can be described: 1) For small N, a body clearly moves through a field in which the mass is concentrated in the other N-1 bodies or 2) For large N the potential is smooth as it is a mean potential generated by all the other particles. For clusters of galaxies, it is unclear if they are in the limit of large or small N.
In the case of large N, we can derive an expression for the relaxation timescale by considering a system of equal mass particles moving through a smooth potential. In this case, we now show that the relaxation timescale increases with increasing N. Figure 3-5 specifies the encounter geometry of two equal mass objects (assumed to be point masses) that gravitationally scatter off one another. For the sake of this derivation, consider the objects as stars and the potential as a collection of equal mass stars (e.g., a galaxy). The physical question we wish to address is what happens to a star as it orbits around a galaxy at some radius and gravitational scatters off of other nearby stars and hence has its velocity perturbed.

|
Figure 3-5: Encounter geometry for two stars which gravitationally scatter of off one another. |
For this approximation we consider all encounters to be small, that is
 v / v << 1.
In this case we can consider the perturbing star, S1, to remain stationary and
that the
perturbed star, S2, remains on a straight line trajectory.
From the geometry of Figure 3-5
we can then specify the force law as
v / v << 1.
In this case we can consider the perturbing star, S1, to remain stationary and
that the
perturbed star, S2, remains on a straight line trajectory.
From the geometry of Figure 3-5
we can then specify the force law as

| (12) |
or since cos(w) = b/r then

| (13) |
We now set the distance X to be vt so that

| (14) |
Remembering that Newton says
F = m
= m
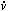
 and
setting s = vt/b (ds / dt = v / b)
and integrating over all time then yields
and
setting s = vt/b (ds / dt = v / b)
and integrating over all time then yields

| (15) |
which can be evaluated to yield

| (16) |
where we see that the perturbation in velocity depends on the initial mass and velocity of the perturbed star and its minimum distance from the perturbing star, which one might have guessed a priori.
Now consider a galaxy of radius R. The surface density of stars in that
galaxy is
N /  R2.
Upon one orbit of the galaxy the star has a number of encounters,
R2.
Upon one orbit of the galaxy the star has a number of encounters,
 n, with impact parameters
in the range b to b + db specified by the following
n, with impact parameters
in the range b to b + db specified by the following
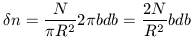
| (17) |
The total number of encounters would be obtained by integrating over db
so note
that if the range of db was from 0 to R one would recover
 n =
N. Since the
perturbations are randomly oriented then
<
n =
N. Since the
perturbations are randomly oriented then
<  v
v > = 0
We are interested in the amplitude of
> = 0
We are interested in the amplitude of
 v
v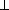 so that
so that

| (18) |
This expression is only valid in the limit where
 v
v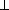 / v
/ v
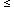 1 which is satisfied
when b = 2Gm /
1 which is satisfied
when b = 2Gm /
 v v
v v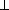
 bmin
where bmin
bmin
where bmin
 Gm / v2. Now integrating
equation 7 over all possible impact parameters, bmin
to R yields
Gm / v2. Now integrating
equation 7 over all possible impact parameters, bmin
to R yields

| (19) |
Defining 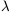
 R / bmin (the ratio of maximum to
minimum impact parameters)
then yields
R / bmin (the ratio of maximum to
minimum impact parameters)
then yields

| (20) |
For a galaxy of equal mass stars we can define the orbital velocity of a star, at some radius R in the galaxy to be v2 = GNm / R. Eliminating R from equation 20 then yields

| (21) |
We are thus lead to the basic result

| (22) |
We operationally define a relaxation time as the amount of time it takes for
 v to be
equal to v. That is, after enough encounters, the perturbations will
be of the same amplitude
as the initial velocity. According to equation 22, this will occur after
a number of encounters
given by N / (8 ln
v to be
equal to v. That is, after enough encounters, the perturbations will
be of the same amplitude
as the initial velocity. According to equation 22, this will occur after
a number of encounters
given by N / (8 ln 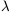 ),
which we define as nrelax. The
relaxation timescale is
then just given by nrelax x tcross where
tcross is the time it takes for the star
to cross (orbit) the galaxy and is equivalent to a dynamical time scale (e.g.,
(G
),
which we define as nrelax. The
relaxation timescale is
then just given by nrelax x tcross where
tcross is the time it takes for the star
to cross (orbit) the galaxy and is equivalent to a dynamical time scale (e.g.,
(G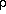 )-1/2). Using the definition of
)-1/2). Using the definition of
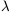 =
R / bmin and
bmin
=
R / bmin and
bmin  Gm / V2 then yields
Gm / V2 then yields
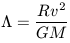
| (23) |
which is just N. So the relaxation time scale is

| (24) |
where tcross is essentially R/V. Hence, although counter-intuitive, long range relaxation times slowly increase with increasing N.
If trelax for some stellar system is larger
than the age of the Universe then the system is said to be collisionless which
means that stars
move under the influence of the mean potential generated by all the other
particles. For instance, a
galaxy has N  1011 and
R/V
1011 and
R/V
 3 x 108. This
yields trelax
3 x 108. This
yields trelax  1018 years which is 8 orders of magnitude older than the universe.
A cluster of galaxies has N
1018 years which is 8 orders of magnitude older than the universe.
A cluster of galaxies has N  103 and R/V
103 and R/V  109. This yields
trelax
109. This yields
trelax  1011 years and hence mass segregation should not be observed
in clusters of galaxies.
1011 years and hence mass segregation should not be observed
in clusters of galaxies.
A full derivation of the two-body relaxation time can be found in Binney and Tremaine (1987). Following that we can express the two-body relaxation timescale via the following parameterized equation:
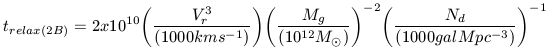
| (25) |
For a very massive galaxy, Mg ~ 1012
M in a dense
galaxy cluster (Nd ~ 1000 galaxies Mpc-3)
the two-body relaxation
time scale is 20 billion years. These conditions describe a cluster like
Coma. In dense clusters like Coma there is evidence
that the most massive/brightest
galaxies have settled to the bottom of the cluster potential (e.g.,
Beers and Geller 1983; Oegerle and Hill 1994). Alternatively,
they could have merely formed in place at that location.
Whether or not long range forces
(equation 24) or two-body relaxation (equation 25) dominates probably
depends upon the mass function of the galaxies in the cluster. A cluster
with a few massive galaxies in it may have the shorter two-body relaxation
timescale in which case those few massive galaxies will migrate to the
center of the cluster potential and remain there. The essential point,
however, is that relaxation times for clusters generally
exceed the expansion age of the Universe
in a dense
galaxy cluster (Nd ~ 1000 galaxies Mpc-3)
the two-body relaxation
time scale is 20 billion years. These conditions describe a cluster like
Coma. In dense clusters like Coma there is evidence
that the most massive/brightest
galaxies have settled to the bottom of the cluster potential (e.g.,
Beers and Geller 1983; Oegerle and Hill 1994). Alternatively,
they could have merely formed in place at that location.
Whether or not long range forces
(equation 24) or two-body relaxation (equation 25) dominates probably
depends upon the mass function of the galaxies in the cluster. A cluster
with a few massive galaxies in it may have the shorter two-body relaxation
timescale in which case those few massive galaxies will migrate to the
center of the cluster potential and remain there. The essential point,
however, is that relaxation times for clusters generally
exceed the expansion age of the Universe
 Collision Timescale: The
collision timescale can be easily
derived by treating a cluster of galaxies as being a thermodynamic
state in a closed volume. In this volume there is number density of
galaxies (Nd), a characteristic cross section
(
Collision Timescale: The
collision timescale can be easily
derived by treating a cluster of galaxies as being a thermodynamic
state in a closed volume. In this volume there is number density of
galaxies (Nd), a characteristic cross section
( Rgal2), and
a characteristic velocity dispersion (V3). The product,
((Nd) (
Rgal2), and
a characteristic velocity dispersion (V3). The product,
((Nd) ( Rgal2) (V3))-1
defines a timescale which is the mean time between
direct collisions of the particles. Dense systems with large galaxies
and high velocity dispersions have shorter collision times. A
convenient parameterization is:
Rgal2) (V3))-1
defines a timescale which is the mean time between
direct collisions of the particles. Dense systems with large galaxies
and high velocity dispersions have shorter collision times. A
convenient parameterization is:
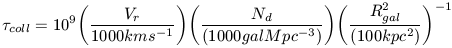
| (26) |
For a galaxy with Rgal ~ 10 kpc, the collision time scale in the dense core of the Coma cluster is, interestingly, comparable to the dynamical timescale! This suggests that galaxy evolution can be severely altered in such a dense environment.
 Cooling Timescale: When cold
gas from a galaxy in a cluster
is liberated from the galaxy potential by some process, that gas
heats up as it comes into virial equilibrium with the cluster potential.
In the case where this gas is an ideal gas, the temperature of that gas is
set up by the virial condition
Cooling Timescale: When cold
gas from a galaxy in a cluster
is liberated from the galaxy potential by some process, that gas
heats up as it comes into virial equilibrium with the cluster potential.
In the case where this gas is an ideal gas, the temperature of that gas is
set up by the virial condition

| (27) |
The observed values of Mcl and V3 predict temperatures in the kev range and we expect most clusters to be filled with an X-ray emitting plasma. The cooling of that plasma is dominated by collisional processes with the hot electrons and the ions. This cooling is primarily done through metallic lines and therefore the heavy element abundance of the plasma is important. The cooling timescale depends upon the electron density ne, the initial temperature, and the cooling coefficient appropriate for a particular gas composition. There is an order of magnitude difference in cooling coefficient for 0.1 solar metallicity gas and primordial (zero metallicity) gas (Silk and Wyse 1993). X-ray spectra of clusters, however, indicate that the ICM has a mean metallicity which is approximately solar. For this case, a convenient expression for the cooling timescale (see also Raymond et al. 1976) is

| (28) |
where T8 is measured the temperature in units of
108 K and
ne is measured in particles per cm-3. Most
clusters have ne 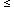 10-3 and hence
when heated to a few T8 K will remain
so over a Hubble time.
10-3 and hence
when heated to a few T8 K will remain
so over a Hubble time.
 Dynamical Friction
Timescale: Dynamical friction is an odd
astrophysical process and can only occur in specialized environments.
It is caused when a smaller mass object passes nearby a larger mass
object which itself is surrounded by a gravitationally bound halo of
uniformly light particles. The typical situation is a large galaxy
surrounded by a halo of 1
M
Dynamical Friction
Timescale: Dynamical friction is an odd
astrophysical process and can only occur in specialized environments.
It is caused when a smaller mass object passes nearby a larger mass
object which itself is surrounded by a gravitationally bound halo of
uniformly light particles. The typical situation is a large galaxy
surrounded by a halo of 1
M stars. If the lower
mass galaxy passes
through this halo, that passage will create a gravitational wake
which causes the low mass stars to line up behind the passing galaxy.
This in turn exerts a small gravitational force on the smaller body
causing it to lose some energy. Dynamical friction represents
a kind of frictional drag which causes the lesser bodies motion to
damp out. If the lesser body is on an orbit that makes repeated passages
through that halo, its orbit will decay over time and it will
spiral in and be acreted by the larger object, thus causing that larger
object to grow in mass and size. During this process, tidal forces
can act to strip more stars out of the lesser body building up the
size of the halo.
stars. If the lower
mass galaxy passes
through this halo, that passage will create a gravitational wake
which causes the low mass stars to line up behind the passing galaxy.
This in turn exerts a small gravitational force on the smaller body
causing it to lose some energy. Dynamical friction represents
a kind of frictional drag which causes the lesser bodies motion to
damp out. If the lesser body is on an orbit that makes repeated passages
through that halo, its orbit will decay over time and it will
spiral in and be acreted by the larger object, thus causing that larger
object to grow in mass and size. During this process, tidal forces
can act to strip more stars out of the lesser body building up the
size of the halo.
Dynamical friction acts as a damping mechanism to remove orbital energy from cluster galaxies. Binney and Tremaine (1987) demonstrate that a galaxy of mass Mg which moves with velocity v experiences a deceleration due to dynamical friction given by

| (29) |
From this, we can make a straightforward derivation of the dynamical friction timescale to see if its a relevant process for clusters of galaxies. The characteristic timescale over which energy is lost via dynamical friction is defined as

| (30) |
where f is a numerical value related to the distribution of the
orbits in the potential,
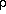 b is the
background density of light
particles (e.g., 1 M
b is the
background density of light
particles (e.g., 1 M stars), vrel is the relative velocity of
the companion galaxy,
stars), vrel is the relative velocity of
the companion galaxy, 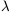 (not
to be confused with the cosmological
constant) is related to the impact parameter bmin as
(not
to be confused with the cosmological
constant) is related to the impact parameter bmin as
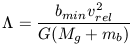
| (31) |
where mb is the mass of the background particles.
For simplicity we assume circular orbits in which case f = 0.4 (see Binney and Tremaine 1987) and a flat rotation curve which satisfies the equation
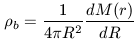
| (32) |
where M(r) follows from the virial theorem as

| (33) |
Substituting this into equation 30 yields

| (34) |
Recalling that  cross =
R / V and parameterizing
Mg by (M / L) Lg and making
use of equation 33 leads to the general
expression for the dynamical friction timescale
cross =
R / V and parameterizing
Mg by (M / L) Lg and making
use of equation 33 leads to the general
expression for the dynamical friction timescale

| (35) |
which expresses the friction timescale as some multiple of the dynamical timescale. In astrophysical units, equation 34 can be written as

| (36) |
Cluster environments in which smaller galaxies have vrel
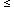 300
km s-1 and distances
300
km s-1 and distances
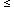 200 kpc have
values of
200 kpc have
values of  df
t are less than H0-1. Hence, there are
situations where
dynamical friction could substantially alter the orbits of cluster
galaxies and change the overall population of the cluster.
But how prevalent is this?
df
t are less than H0-1. Hence, there are
situations where
dynamical friction could substantially alter the orbits of cluster
galaxies and change the overall population of the cluster.
But how prevalent is this?
In a study of central cluster environments, Bothun and Schombert (1990) suggest that 25% of all rich clusters are experiencing an augmentation to the luminosity/mass of the central dominant galaxy as dynamical friction causes the orbits of these central cluster galaxies to decay. Further support for this process comes from the observation that many galaxies in the central regions of clusters appear to have truncated surface brightness profiles. This is most likely due to the tidal liberation of stellar material during the close passage to the central dominant cluster galaxy. In order to prevent the entire depletion of this population over a Hubble time, it is necessary that the galaxies currently in the centers of these clusters are on relatively elongated orbits. For most galaxy clusters, dynamical friction is avoided if the orbits of the individual members are highly radial. Studies of other galaxy clusters by Gebhardt and Beers (1991) and Merrifield and Kent (1991) have reached similar conclusions.